Определение, геометрический и механический смысл двойного интеграла. Теорема существования

Пусть функция 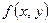непрерывна в ограниченной замкнутой области D. Разобьем эту область произвольным образом на n частей 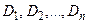(рис. 1), которые будем называть элементарными областями и площади которых обозначим 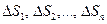. В каждой области 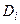выберем произвольно точку 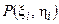, 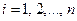. Для всех 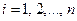вычислим 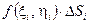и просуммируем эти выражения по от 1 до 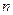. В результате получили так называемую интегральную сумму

.

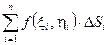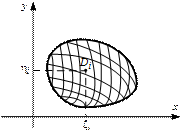
Рис. 1.

Если функция 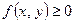и имеет смысл плотности, распределенной в области D, то при достаточно малыхэлементарных областях 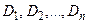составленная интегральная сумма приближенно равна массе тонкой плоской пластины, занимающей область D.

.

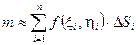Очевидно, что точный результат мы получим, если будем бесконечно увеличивать число областей, на которые делится область D. Причем число элементарных областей так, чтобы каждая область 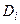стягивалась в точку.

Для этого введем ранг дробления 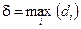, где 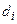- диаметр области .

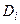Дата добавления: 2014-01-20