Решение. Дивергенцией векторного поля в точке дифференцируемости называется скалярная величина, которая обозначается

Определение

Дивергенцией векторного поля 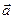в точке дифференцируемости 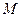называется скалярная величина, которая обозначается и которая вычисляется по формуле

.

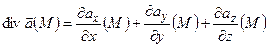Задача

Вычислите дивергенцию векторного поля 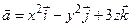в точке .

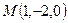Дивергенция векторного поля в произвольной точке дифференцируемости поля равна:

.

Вычислим значение дивергенции в точке .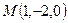

.

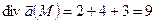Теорема Гаусса – Остроградского

Если координаты векторного поля 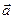, т.е. функци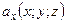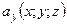и ; и - непрерывны в области 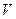, ограниченной поверхностью , вместе со своими частными производными первого порядка, то поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции этого поля по области .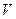

,

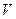где – граница области и нормаль 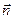– внешняя.

Дата добавления: 2014-01-20