II. Схемы дедуктивных умозаключений

Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (2), в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?

В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. Для этого предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие:

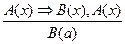
– правило заключения; 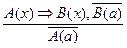– правило отрицания;

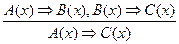– правило силлогизма.

В начальном курсе математики для доказательства используют только правило заключения (см. пример 1).

Дедуктивные рассуждения (умозаключения) с большей или меньшей строгостью следует использовать при изучении начального курса математики, т. к. именно они воспитывают строгость, четкость, лаконичность мышления. Особенность дедуктивных рассуждений заключается в их тесной связи с индуктивными. А так же – то, что в нач. кл. они применяются в неявном виде, т. е. общая и частная посылка в большинстве случаев не проговариваются, уч-ки сразу приступают к действию, которое соответствует заключению. Для сознательного проведения дед. рассуж. необходима большая подготовительная работа, направленная на сознательное усвоение общего вывода, свойства, закономерности. Этого требуют особенности мышления мл шк., которое отличается конкретностью. Но сознательное усвоение общего вывода позволяет пользоваться дедуктивным рассуждением.

При решении простых задач на разностное сравнение имеет смысл уже обращаться к дедуктивным рассуждениям, используя наглядность только на этапе проверки решения задачи. Например: «У Коли было 6 марок, у Пети 2 марки. На сколько марок больше у Коли, чем у Пети?» Рассуждения уч-ся: «Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньше (общая посылка). Умозаключение: значит, нужно из марок Коли вычесть марки Пети».

Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности, свойства в общем виде, связанная с развитием математической речи учащихся. Например, довольно длительная работа по усвоению принципа построения натурального ряда чисел позволяет учащимся овладеть правилом: «Если к любому числу прибавить 1, то получим следующее за ним число; если из любого числа вычтем 1, то получим предшествующее ему число». Составляя таблицы € + 1 и € – 1, ученик фактически пользуется этим правилом как общей посылкой, выполняя тем самым дедуктивные рассуждения. Примером дедуктивных умозаключений в начальном обучении математике является и такое рассуждение: «4<5 потому, что 4 при счете называется раньше, чем 5». В данном случае общая посылка: если одно число называется при счете раньше другого, то это число меньше; частная посылка: 4 при счете называют раньше, чем 5; заключение: 4<5.

Дедуктивные рассуждения имеют место в начальном курсе математики и при вычислении значений выражений. В качестве общей посылки выступают правила порядка выполнения действий в выражениях, в качестве частной посылки – конкретное числовое выражение, при нахождении значения которого учащиеся руководствуются правилом порядка выполнения действий.

Анализ школьной практики позволяет сделать вывод о том, что для формирования у школьников умений рассуждать не всегда используются все методические возможности. Например, при выполнении задания:

Сравни выражения, поставив знак <, > или =, чтобы получилась верная запись: 6+3... 6+2 6+4... 4+6 учащиеся предпочитают заменять рассуждения вычислениями: «6+2 < 6+3, потому что 8<9». Этим ответ ограничивается, так как суждение «8<9» чаще всего не обосновывается. Хотя при выполнении данного задания они могли бы сравнить слагаемые в суммах и сделать умозаключение о том, какой следует поставить знак, не прибегая при этом к вычислениям. Интересный опыт работы по формированию умения рассуждать отражен в опыте работы учителя В.П. Леховой. Она предлагала детям два листа, на одном из которых были написаны общие посылки, на другом – частные. Нужно установить, какой общей посылке соответствует каждая частная. Ученикам дается инструкция: «Вы должны выполнить каждое задание на листе 2, не прибегая к вычислениям, а лишь воспользовавшись одним из правил, записанных на листе 1».

Лист 1

1. Если уменьшаемое увеличить на несколько единиц, не изменяя при этом вычитаемого, то разность увеличится на столько же единиц.

2. Если делитель уменьшить в несколько раз, не изменяя при этом делимого, то частное увеличится во столько же раз.

3. Если одно из слагаемых увеличить на несколько единиц, не изменяя при этом другое, то сумма увеличится на столько же единиц.

4. Если каждое слагаемое делится на данное число, то сумма тоже разделится на это число.

5. Если из данного числа вычесть предшествующее ему число, то получим 1.

Лист 2

Задания расположены в другой последовательности, чем посылки.

1. Найди разность: 84 – 83, 32 – 31, 54 – 53.

2. Назови суммы, которые делятся на 3:

9+27, 6+9, 5+18, 12+24, 3+4, 3+6.

3. Сравни выражения и поставь знаки <, > или =:

125–87... 127–87 246–93... 249–93

584–121... 588–121

4. Сравни выражения и поставь знаки <, > или =:

304: 8... 304:2 243:9... 243:3 1088:4... 1088:2

5. Как быстро найти сумму второго примера в каждом столбике:

25+13=38 134+28=162 257+375=632

27+13= … 139+28= … 257+378= …

Таким образом, дедуктивные рассуждения могут являться одним из способов обоснования истинности суждений в начальном курсе математики. Учитывая, что они доступны не всем младшим школьникам, в начальных классах используются и другие способы обоснования истинности суждений, которые в строгом смысле нельзя отнести к доказательствам. К ним относятся эксперимент, вычисления и измерения.

Вопрос 4. Понятие текстовой задачи, её структура. Основные этапы решения задачи и приёмы их выполнения. Методика формирования понятия «задача» в начальном курсе математики. Различные методические подходы к формированию умения решать задачи.

Задача – сформулированный словами вопрос, ответ на который можно получить, выполнив определённый набор операций (Истомина Н.Б.). В начальном курсе математике решению текстовых задач уделяется огромное внимание, так как они являются не только средством формирования многих математических понятий, но и средством формирования умений строить математические модели реальных явлений, а также средством развития мышления детей.

Текстовая задача – описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения (Стойлова Л.П.)

Текстовая задача содержит 2 основных элемента:

1) условие задачи -утверждение задачи. В задаче обычно не одно условие, а несколько. Они представляют собой количественные и качественные характеристики объектов задачи и отношений между ними.

2) требование задачи – Их может быть несколько. Они могут быть сформулированы как в вопросительной, так и в утвердительной форме.

Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Чтобы понять структуру задачи, надо построить высказывательную модель задачи.

Этапы решения задачи.

Дата добавления: 2014-01-20