Упражнения для закрепления

1. Каких элементов больше?

На сколько?

Каких элементов меньше?

На сколько?

2. На тарелке лежит 10 яблок и 4 апельсина. На сколько апельсинов меньше, чем яблок? Реши задачу с помощью рисунка.

3. Придумай задачу, опираясь на условный рисунок, и реши ее.

4. 8-6 Нарисуй схематический чертеж к этому выражению.

5. Составь задачу, для решения которой нужно из 15 вычесть 9. Сделай чертеж

Вопрос 6. Определение отношений "больше в … раз" и "меньше в … раз" для натуральных чисел, их теоретико-множественный смысл и способы моделирования. Методика формирования понятий "больше в … раз" и "меньше в … раз" в начальном курсе математики. Обучение младших школьников решению текстовых задач с данными отношениями

С теоретико-множественной точки зрения можно рассмотреть смысл отношений "больше в" и "меньше в ", с которыми младшие школьники встречаются при решении текстовых задач. В аксиоматической теории определение этих отношений вытекает из определения деления натуральных чисел: если a:b=c, то можно говорить, что " a больше b в c раз" или, что" b меньше a в c раз". И чтобы узнать, во сколько раз одно число больше или меньше другого, достаточно большее число разделить на меньшее, если a=n(A), b=n(B) и известно, что " a меньше b в c раз", и поскольку a<b, то во множестве B можно выделить собственное подмножество, равномощное множеству A, но так как a меньше b в c раз, то множество B можно разбить на c подмножеств, равномощных множеству A. Так как c -это число подмножеств в разбиении множества B, содержащего b элементов, а в каждом подмножестве- a элементов, то c=b:a. Теоретико-множественным смыслом отношения " a больше (меньше) b в с раз" можно воспользоваться при обосновании выбора действий при решении задач.

A – грядки с морковкой

В – грядки с картошкой

Пример: "На участке 3 грядки моркови, грядок картошки в 2 раза больше. Сколько грядок картошки на участке?"

В задаче идет речь о двух множествах: множестве грядок моркови (А) и множестве грядок картошки (В). Известно, что n(A)=3, и что в множестве В элементов в 2 раза больше, чем в множестве А. Требуется найти число элементов в множестве В, то есть n(В).

Так как во множестве В элементов в 2 раза больше, чем во множестве А, то множество В можно разбить на 2 подмножества, равномощных множеству А. Поскольку в каждом из подмножеств содержится по 3 элемента, то всего во множестве В будет 3+3 или 3•2 элементов. Выполнив вычисления, получаем ответ на вопрос задачи: на участке 6 грядок картошки.

Смысл умножения тесно связан с понятием «увеличить в несколько раз». Важно разъяснить детям, что запись 2 • 5 можно прочитать: «2 повторить 5 раз», «по 2 взять 5 раз», «2 умножить на 5», «2 увеличь в 5 раз». В различных программах математики этот вопрос решается по-разному.

В учебнике М2М вводится понятие «больше в» и «меньше в» одновременно. Это можно сделать только после того, как дети познакомятся с делением. Работа над усвоением смысла умножения и понятием «больше в» значительно разведена во времени. Для введения понятия «больше в», «меньше в» используется комментирование рисунка. Например, к рисунку дано пояснение: «Квадратов – 3, кружков – 4 раза по 3. Кружков в 4 раза больше, чем квадратов, а квадратов в 4 раза меньше, чем кружков». Потом учащиеся выполняют задание: Сделай рисунок и реши задачу: «Для детей детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили?». Последующая работа по усвоению понятий «больше в», «меньше в» связана с решением простых задач на предметном уровне. Для того чтобы дети не путали понятие «больше в», «меньше в», им предлагается задание: "Сделай рисунок и реши задачу:

1. Сережа вырезал 4 красных квадрата, а синих в 3 раза >, чем красных. Сколько синих квадратов вырезал Сережа?

2. Зина вырезала 4 красных квадрата, а синих на 3 квадрата >, чем красных. Сколько синих квадратов вырезала Зина?"

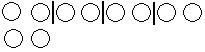
Формирование представлений о смысле деления связано с введением понятий "уменьшить в несколько раз" ("меньше в") и "кратное сравнение" ("во сколько раз меньше?", "во сколько раз больше?"). Для усвоения также используются действия с предметными множествами. Однако деятельность учащихся может быть организованна по-разному. При одном подходе (М3М) дается образец действия. Предлагается рисунок и комментируется так: "В 1-ом ряду 8 кружков, а во втором в 4 раза меньше. Чтобы получить в 4 раза меньше кружков, чем 8, разделили 8 кружков на 4 равные части и взяли столько, сколько их в одной части. Сколько кружков положили во второй ряд?"

При другом подходе (М3И) учащимся предлагается два рисунка, которые они должны сравнить, ответив на вопросы: "Что изменилось слева направо? Что изменилось справа налево?

Ответы: «Слева 3 круга, а справа 3 круга повторили 4 раза». Этот ответ соотносится с 3 • 4, т.е. данная запись отражает те изменения, которые произошли с левым рисунком «Справа на 9 кругов больше, чем слева». Это высказывание соотносится с 3 + 9, которое учащиеся связываю с понятием, «увеличить на». Возникает вопрос, как увеличиться 3, если его повторить 4 раза. Говорят, что 3 увеличили в 4 раза. Далее учащиеся высказывают предположение о том, что выражение 12:4 связано с понятием "уменьшения в". Для обоснования этого предположения они используют рисунок. Справа 12 кругов. Если разделить их на 4 равные части, то в каждой части получим в 4 раза меньше.

Вводится это понятие по программе М _(1-4) в 3 классе (стр. 52) - индуктивно. То есть рассматривается сначала теоретико-множественный смысл на наглядном материале, далее анализируем, вследствие чего во время беседы выявляются отношения, которые указаны в правиле, а далее предоставляем систему закрепляющих упражнений:

А

А

1. Что ты можешь сказать о длине отрезков в каждой паре?

B

N

B

N

M

M

С помощью циркуля и линейки учащиеся отвечают на поставленный вопрос, используя понятия «больше в», «меньше в», «больше на» и «меньше на».

2. Нарисуй фигуру, которая в 2 раза меньше данной фигуры.

3. Догадайся! (М2И) Какой паре рисунков соответствует выражение 18:3 и что оно обозначает?

Выражение 18:3 обозначает, сколько раз в 18 клетках содержится по 3 клетки. В этом случае говорят, что выражение 18:3 обозначает, во сколько раз больше клеток в первом прямоугольнике, чем во втором, и во сколько раз меньше клеток во втором прямоугольнике, чем в первом.

Подумай! Какие выражения ты запишешь, чтобы ответить на вопросы:

Во сколько раз в первом прямоугольнике клеток больше, чем во втором?

Во сколько раз в третьем прямоугольнике клеток меньше, чем в первом?

4. Во сколько раз площадь верхней фигуры больше площади нижней?

А) Б)

А

Запиши ответ числовым равенством.

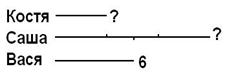
5. "Костя нашел ракушек в 3 раза меньше, чем Саша, а Вася в 2 раза меньше, чем Саша. Сколько ракушек нашел Саша, если Вася нашел их 6? Сколько ракушек у Кости?"

Начерти схему и запиши решение задачи по действиям.

1) 6•2=12 (р.) – нашёл Саша;

2) 12:3=4 (р.) – нашёл Костя

Вопрос 7. Понятие разбиения множества на попарно непересекающиеся подмножества (классы). Отношение эквивалентности и его связь с разбиением множества на классы. Использование приема классификации при обучении математике в начальных классах.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы х₁,х₂…х_n, если выделена система подмножеств, отвечающая требованиям:

1) подмножества х₁,х₂…х_n попарно не пересекаются;

2) объединение подмножеств х₁,х₂…х_n совпадает с множеством Х.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, из множества треугольников выделить подмножество равносторонних, разносторонних и равнобедренных треугольников. Разбиения не будет, так как равносторонние треугольники являются равнобедренными треугольниками.

Рассмотрим множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа обладающие свойствами "быть кратными 3". Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, то есть, получаем еще одно подмножество натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса. Если на множестве Х задано одно свойство, то это множество разбивается на 2 класса:

1. класс объектов обладающих этим свойством;

2. дополнение 1-ого класса до множества Х

Такую классификацию называют дихотомической.

Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности. Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности). Теорема. Множество считается разбитым на классы тогда и только тогда, когда на нем задано отношение эквивалентности.

Вообще же существование отношения эквивалентности является важным принципом математики так как:

1. Эквивалентный, следовательно, равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемы.

2. Поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, то есть произвольным элементом этого класса.

3. Разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий.

Прием классификации.

Умение выделять признаки предметов и устанавливать между ними сходство и различие – основа приема классификации.

Прием классификации – это прием разбиения множества на классы. В начальной школе можно использовать следующие упражнения, которые бы могли разделяться на разные виды:

1. Подготовительные задания. К ним относятся:

Убери (назови) "лишний" предмет (число). Назови лишнее число (пример):

8; 6; 3; 2; 10 6+1; 8+1; 3+5; 9+4; 2+7

"Нарисуй предметы такой же формы до равного количества". Сюда же можно отнести задание на развитие внимания и наблюдательности: "Какой предмет убрали?", "Что изменилось?"

2. Задания, в которых на основание классификации указывает учитель: 37; 61; 57; 34; 81; 64; 27 – разбейте данные числа на три группы, ориентируясь на цифры, записанные в разряде единиц; – на две группы, ориентируясь на цифры, записанные в разряде десятков.

3. Задания, при выполнении которых дети сами выделяют основание классификации. Переходя к таким упражнениям полезно указывать количество групп разбиения.

– разбейте данные выражения на группы; – на две группы; – на четыре группы;

3+2; 6-3; 4+5; 9-2; 4+1; 7-2; 10-1; 6+1; 3+4

В качестве основания для разбиения выражений на группы может выступать и вычислительный прием. Для этого можно использовать следующие задания:

По какому признаку можно разбить данные выражения на две группы 57+4; 23+4; 36+2; 75+2; 68+4; 52+7; 76+7; 44+3; 88+6; 82+6

Если учащиеся не могут увидеть нужное основание для классификации, то учитель может помочь им следующим образом: "В одну группу я запишу 57+4, в другую 23+4, в какую вы запишите выражение 36+9".

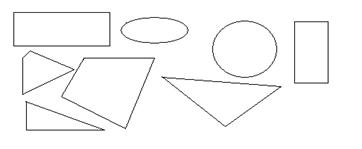
Психологи утверждают, что, так как основой формирования у детей представления о геометрических фигурах является способность к восприятию формы, что позволяет ребенку различать и изображать различные геометрические фигуры, то достаточно показать ему ту или иную геометрическую фигуру и назвать ее соответствующим термином. Классификация геометрических фигур как прием введения понятия "прямоугольник":

1. Уберите фигуры, не имеющие прямых углов.

2. Из оставшихся выберите фигуры, имеющие хотя бы один прямой угол.

3. Из оставшихся выберите фигуры, у которых все углы прямые.

Применение приема классификации на уроках позволяет значительно расширить имеющиеся в практике приемы работы, способствует формированию положительных мотивов в учебной деятельности, так как подобная работа содержит и элемент игры и элемент поисковой деятельности, что в свою очередь повышает активность учащихся и обеспечивает самостоятельное выполнение работы.

Вопрос 8. Определение числовой функции. Способы задания функции. Прямая и обратная пропорциональности, их свойства и графики. Методика обучения решению задач с прямо пропорциональными и обратно пропорциональными величинами.

В школьном курсе математики основное внимание уделяется числовым функциям. Причиной этого является тесная связь математики с естественными науками, в частности, с физикой, для которой числовые функции служат средством количественного описания различных зависимостей между величинами. В начальном курсе математики понятие функции и всё, что с ним связано, в явном виде не изучается.

Числовой функцией называется такое соответствие между числовыми множествами Х и R, при котором каждому числу из множества Х сопоставляется единственное число из множества R.

Для задания функции необходимо указать, во-первых, числовое множество Х, т.е. область определения функции, и, во-вторых, правило, по которому каждому числу из множества Х соответствует единственное действительное число. Существует 2 способа задания функций:1 – перечисление всех пар, участвующих в функциональном соответствии. Приёмы: график в прямоугольной (декартовой) системе координат, таблица. 2. – указание характеристического свойства (вербально – словесно или аналитически – формулой у = f(x)). Числовые функции можно представить наглядно на координатной плоскости.

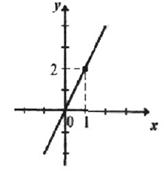
Графиком функции у=2x-3, заданной на множестве R, является прямая, а графиком функции у= х², заданной также на множестве R, – парабола.

Прямой пропорциональностью называется функция, которая может быть задана при помощи формулы у=kx, где k не равное нулю действительное число.

Пример: Если в одном пакете муки 2кг, а куплено x таких пакетов, то всю массу купленной муки (обозначим её через y) можно представить в виде формулы y=2x, т. е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k=2.

Дата добавления: 2014-01-20