Современных условиях хозяйствования

Доля –одна из равных частей целого. Дробь –совокупность нескольких долей. В записи дроби m/nчисла mи nназываются m – числителем, n – знаменателем. Дробь m/n называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему. Дроби, являющиеся численным значением одной и той же величины, называются равными.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь равная данной. На этом свойстве основано 2 операции с дробями:

а) сокращение дроби – это замена дроби ей равной, но с меньшими числителем и знаменателем;

б) приведение дробей к общему знаменателю – это замена дробей им равными, но с одинаковым знаменателем.

Если числитель и знаменатель дроби взаимно простые числа, т.е. одновременно делятся только на единицу, то дробь называется несократимой.

Для того чтобы дроби m/n и p/q выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство mq=np Þ две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.

Отношение равенства дробей рефлексивно (m/n=m/n, т.к. mn=nm), симметрично (если m/n=p/q, то p/q=m/n, т.к. mq=npÞpn=qm) и транзитивно (если m/n=p/q и p/q=r/s, то m/n=r/s), т.е. является отношением эквивалентности. На множестве рациональных чисел отношение эквивалентности можно задать двуместным предикатом: Р(x;y)=«дробь х=дроби у». Это отношение разбивает множество рациональных чисел на классы эквивалентных (равных) дробей. Каждый класс данного разбиения есть положительное рациональное число. Положительное рациональное число – это класс равных дробей, где каждая дробь этого класса есть запись положительного рационального числа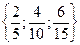. Среди равных между собой дробей всегда существует одна единственная несократимая дробь. Количество классов эквивалентности дробей и количество дробей в каждом классе бесконечно. Множество всех п.р.ч. обозначают Q₊. Отношение равенства: если п.р.ч. а представлена дробью m/n, а п.р.ч. в – p/q, то а=в тогда и только тогда, когда mq=npÞравные рациональные числа представляются равными дробями.

Если п.р.ч. а представлено дробью m/n, а п.р.ч. в – дробью p/n, то их суммой называется число а+в, которое представляется дробью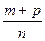. Сложение п.р.ч. коммутативно и ассоциативно.

Если п.р.ч. а представлено дробью m/n, а п.р.ч. в – дробью p/q, то их произведением называется число ав, которое представляется дробью 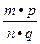. Умножение п.р.ч. коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания.

Вычитание п.р.ч. удовлетворяет условию: а-в=с тогда и только тогда, когда а=в+с. Равность а-в п.р.ч. существует тогда и только, когда в < а. Если разность а-в существует, то она единственна. Правило вычитания: .

Деление удов. условию: а:в=с тогда и только, когда а=вс

Правило деления: 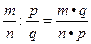Þ частное п.р.ч. существует всегда!

Согласно программе начального курса математики при изучении темы «Доли» ставятся следующие задачи:

§ сформировать у учащихся представление о доле величины;

§ научить читать и записывать доли;

§ научить сравнивать доли одной и той же величины на наглядной основе;

§ решать задачи на нахождение доли числа и числа по его доле.

Для формирования представления о дроби используется решение текстовых задач. Сначала предлагается задача: «Два брата разделили поровну между собой 6 яблок. Сколько яблок досталось каждому?»

Ученики самостоятельно записывают решение задачи (6:2=3) и дают ответ на ее вопрос, объясняя выбор арифметического действия. Далее предлагается следующая задача: «Два брата разделили между собой 1 яблоко поровну. Сколько яблок досталось каждому брату?». Учитель берет яблоко и просит разделить его поровну. Ученики предлагают разрезать яблоко на две равные части. Учитель разрезает яблоко и показывает одну из равных частей. Спрашивает: как можно назвать эту часть яблока (половина). Почему? (разделили пополам). Кто догадался, как можно по-другому назвать половину? (одна вторая). Докажите. После этого дети отвечают на вопрос задачи.

Одна вторая – это дробное число: ½. На доске оформляется решение задачи: 1:2=1/2 ???.

Далее поясняется, что в записи дроби ½ число под чертой показывает, на сколько равных частей делят предмет. Это знаменатель дроби. Число над чертой показывает, сколько таких частей взяли. Это числитель дроби.

Чтобы научить детей сравнивать дроби на основе наглядности, можно использовать элементы самоконтроля. На доске нарисованы отрезки, разделенные на равные части различным образом.

Убедившись в том, что у учеников сформировались представления о дроби и умение сравнивать дроби с опорой на наглядность, вводятся дроби с числителем, большим единицы. Для этого предлагается задача: «Мама к чаю подала торт, разрезанный на 10 равных кусков. Брат съел 2 куска торта, а сестра съела одну часть. Какую часть торта съел брат? Сестра? Для решения используем круг, разделенный на 10 равных частей:

1. На сколько равных кусков мама разрезала торт?

2. Сколько съела сестра? Покажите.

3. Какую часть торта составляет один кусок?

4. Кто может записать соответствующую дробь?

5. Сколько съел брат?

6. Какую часть торта составляют два куска?

7. Кто может записать дробь две десятых?

Назовите знаменатель, числитель этой дроби. Что они означают?

Затем учащиеся выполняют сравнение дробей с опорой на наглядность и записывают:

1/10<2/10; 2/10>1/10

Кому из детей досталось больше (меньше) торта? Сколько всего кусков съели дети? Какую часть торта составляют съеденные куски? Запишите.

Выполнение этого задания вызывает интерес у класса.

Далее ведется работа по изучению тем: «Нахождение доли числа и нахождение числа по доли».

Вначале учащимся предлагается задача: «Береза прожила 50 лет, что составляет 1/5 часть продолжительности ее жизни. Какова продолжительность жизни березы?»

На доске модель задачи. Дети рассуждают: 1/5 часть составляет 50 лет, а в целом 5 таких частей. Можно узнать продолжительность жизни березы, для этого 50•5=250

Учитель предлагает составить задачу, обратную данной «Продолжительность жизни березы 250 лет. Она прожила одну пятую часть своей жизни. Сколько лет прожила береза?». Составленную задачу дети решают самостоятельно. Получив ответ, они убеждаются в правильности решения исходной задачи.

Рассмотренная методика доказывает, что применение нестандартных учебных заданий при изучении темы способствует активизации деятельности и интереса учащихся к изучаемому материалу.

Методы и приемы работы учителя:

· Наглядный метод – ведущий, иллюстрирует все основные положения;

· Практическая деятельность детей – на закрепление (выделение доли, перегибание, штриховка)

· Большая роль – система закрепляющих упражнений, которые может составить сам учитель, так как в учебниках мало материала;

· Полезно использовать эвристические беседы, кот следует продумывать так, чтобы дети сами делали выводы.

Материал темы в программе:

Моро М.И. 3 класс, тема: Умножение и деление – нахождение доли числа и части по его доле.

Моро М.И. 4 класс, тема: Умножение и деление – задачи на нахождение нескольких долей числа.

Материал темы в учебниках:

Моро М.И. 3 класс 1 часть.

1 урок: стр. 96 – 8 заданий, «Доли». Дети узнают, как образуются, называются, сравниваются дроби с опорой на бытовые представления о делении поровну. Дается определение доли: одна из равных частей целого, показывается запись: 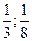. Дети узнают, что означает числитель и знаменатель, учатся сравнивать доли с опорой на наглядный материал (стр.97), стр. 102 – закрепление.

2 урок: стр. 98 – решение задач.

Моро М.И. 4 класс 2 часть – стр.103 «Материал для углубления знаний о долях». Образование долей и дробей, запись и сравнение, задач нет.

Истомина Н.Б.4 класс – стр. 212 – Образование дробей, название, запись, определение, что означает числитель и знаменатель. Особенность – все называют дробями, отсутствует термин доля. Решение задач на дроби – много заданий.

1.1 Понятие хозяйственного учета, его виды и роль в управлении

экономическим субъектом

Организационные структуры хозяйственной деятельности достаточно четко подразделяются на объекты управления и органы управления. Первые состоят из различных хозяйственных подразделений, их объединений, в которых и совершается хозяйственная деятельность. Вторые обеспечивают наблюдение и контроль за хозяйственной деятельностью, ее планирование и регулирование, выполняют функции управления. Объекты управления и органы управления находятся между собой в определенной связи (прямая и обратная) и представляют собой систему управления. Планирование и регулирование обеспечивают прямые связи между органом и объектом управления. Учет, анализ и контроль формируют информацию обратной связи в системе управления. Продуктом управления являются управленческие решения, обеспечивающие достижение целей хозяйственной деятельности. Управление осуществляется на основе полученной информации. Хозяйственный учет – одна из наиболее информационных систем в управлении экономикой хозяйства.

Дата добавления: 2014-01-20