Трение на наклонной плоскости

Парах

Трение скольжения. Трение в поступательных кинематических

Учет трения в механизмах

По физическим особенностям различают трение внутреннее и внешнее.

Внутреннее трение – это процессы, происходящие в твердых, жидких и газообразных телах при их деформации и приводящие к необратимому рассеянию механической энергии. Внутренне трение проявляется в затухании свободных колебаний.

Внешнее трение – это сопротивление относительному перемещению, возникающему между двумя телами в зонах соприкосновения поверхностей, то есть в кинематических парах. По кинематическому признаку различают: трение скольжения, возникающее при скольжении одного тела по поверхности другого, и трение качения, возникающее при качении одного тела по поверхности другого.

При определении сил трения используется известная из физики зависимость, показывающая, что сила трения пропорциональна нормальной реакции (закон Амонтона-Кулона). При этом коэффициент пропорциональности зависит от материалов, физического состояния соприкасающихся поверхностей и называется коэффициентом трения скольжения (коэффициент трения обозначается f и является справочным материалом).

F_f =R^N. f

Геометрическая сумма нормальной реакции и силы трения представляет собой полную реакцию между соприкасающимися поверхностями. Угол между полной реакцией R и нормальной составляющей называется углом трения (обычно обозначается греческой буквой r - рисунок 20 а, в некоторых случаях – j).

Из рисунка 20а:

tg r=F_f /R^N =R^N. f/R^N =f,

то есть

f=tg r, или r=arctgf.

Таким образом, между коэффициентом трения и углом трения очень простая однозначная зависимость, которая позволяет в равной степени пользоваться обоими параметрами для характеристики сил трения и получать наиболее удобные зависимости при расчетах.

При движении тела по поверхности в разных направлениях полная реакция меняет свое положение, а ее геометрическое место представляет собой конус, который называется конусом трения (см. рисунок 20 б).

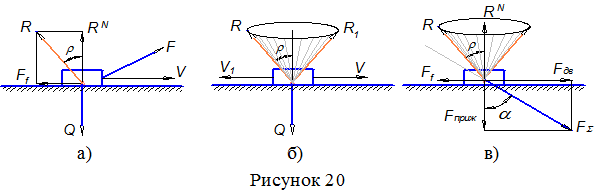
Заменим силы Q и F (рисунок 20 а) результирующей силой F_S (рисунок 20 в). На расчетной схеме обычно все силы прикладывают в центр ползуна, рассматривая сходящуюся систему сил для упрощения задачи и пренебрегая незначительным расстоянием от поверхности до центра ползуна.

Тело будет двигаться вдоль поверхности, если движущая сила F_дв будет больше силы сопротивления (в данном случае силы трения) или, в крайнем случае, равна ей. Из рисунка 20 в:

F_дв= F_S^. sina; R^N = F_приж= F_S^. cosa; F_f = R^N. f = F_S^. cosa ^. f,

условие движения:

, , ,

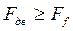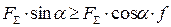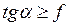но

f=tg r, т.е. 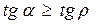или .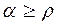

Таким образом, тело будет двигаться вдоль поверхности в том случае, когда линия действия внешней результирующей силы, приложенной к этому телу, будет проходить вне конуса трения (ускоренное движение) или совпадать с его образующей (равномерное движение).

Если линия действия результирующей внешней силы проходит внутри конуса трения, то происходит самоторможение.

В технике для выигрыша в силе часто используется наклонная плоскость. При этом снижается коэффициент полезного действия из-за наличия трения между поверхностями. Рассмотрим общий случай движения тела, нагруженного вертикальной силой Q, вверх по наклонной плоскости под действием силы F, направленной под углом d к направлению движения. Угол наклона плоскости a (рисунок 21).

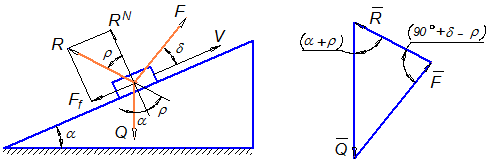
Рисунок 21

Заменим силу трения и нормальную реакцию результирующей реакцией R. Тогда рассматриваемое тело находится под действием трех сходящихся сил: R, Q и F. Равномерное движение – это равновесное состояние, поэтому при равномерном движении векторная сумма этих сил равна нулю:

.

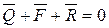На рисунке 21 приведен векторный треугольник, построенный на основании этой векторной суммы. Из приведенного треугольника по теореме синусов легко определяется зависимость между силами Q и F:

Q/sin(90⁰+d –r) =F/sin(a+r) или Q/cos(r–d)=F/sin(a+r).

Отсюда общее условие движения (не только равномерного) тела вверх по наклонной плоскости имеет следующий вид:

Интерес представляет частный случай, когда движущая сила направлена горизонтально (рисунок 22).

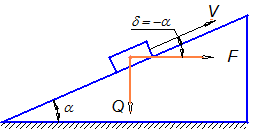
Рисунок 22

Этот случай описывает работу винтовой пары. Он получается подстановкой в общую формулу значения угла d =- a. В результате условие движения тела вверх по наклонной плоскости под действием горизонтальной силы описывается следующим выражением:

.

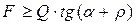Дата добавления: 2014-01-20