Линейные уравнения n-го порядка

Уравнения высших порядков

1) ; надо n-раз проинтегрировать

2) надо пытаться получить порядок интегрирования

Из 1-го уравнения 2-го порядка, получаем 2 уравнение 1-го порядка

3)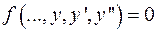(явно отсутствует «x»)

Введем новую функцию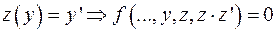

Новая переменная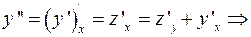

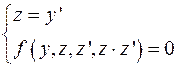
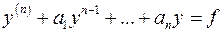(ЛНУ)

функции от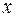

(ЛОУ)

Можно определить линейный дифференциальный линейный оператор

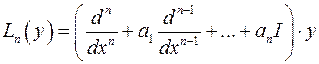
1)Если решаем однородное уравнение

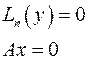
То есть ищем ядро оператора

1)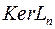- линейное пространство

2)- размерность

По ТСЕ решение уравнения зависит от n произвольных постоянных

Пусть 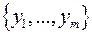базис

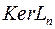
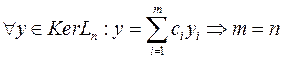
Базис 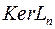называется фундаментальной системой решений (ФСР).

2) Если решаем неоднородное уравнение ;

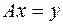
Мы должны уметь обращать оператор

Надо подобрать какое-нибудь (частное решение)

Пусть это будет 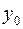, тогда общее решение этого же уравнения

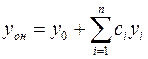- структура общего решения ЛНУ

3) Линейное уравнение с постоянными коэффициентами

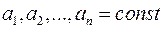
С каждым дифференциальным оператором связок характеристический полином.

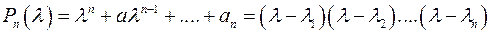
где - корни.

Аналогично разложим дифференциальный оператор на множители

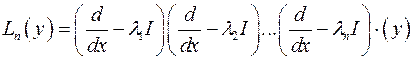
Пример

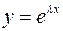- решение

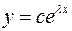- общее решение

Вывод: если 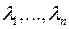- корни характеристического полинома, то 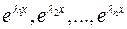- решения ЛОУ

а) предположим, что все корни различны, тогда все - различные функции (если они линейно независимы, то образуют ФСР)

- общее решение ЛОУ.

Дата добавления: 2014-01-20