Функции полезности

Базовая модель рационального поведения

Модель принятия оптимальных решений.

История теории игр.

В 1911 г. Э. Цермело описал теоретико-игровой подход к шахматной игре. В 1921г. Э. Борель начал систематическое изучение матричных игр. В 1928г. вышла работа Дж. Фон-Неймана «К теории стратегических игр», содержащая основные идеи современной теории игр. В 1943г. после публикации книги Дж. Фон-Неймана и О Моргенштерна «Теория игр и экономическое поведение» теория игр окончательно сформировалась как самостоятельная наука.

В настоящем разделе описываются два «варианта» модели рационального поведения субъекта, осуществляющего выбор. В первой модели предпочтения моделируются функцией полезности, и рациональность поведения заключается в стремлении выбора альтернатив, максимизирующих полезность. Во второй модели предпочтения моделируются бинарным отношением предпочтения, и рациональность поведения заключается в стремлении выбора недоминируемых с точки зрения этого отношения предпочтения альтернатив.

Как описывается поведение человека? В экономике с середины XIX века существует концепция максимизации полезности, т.е. концепция экономического человека (homo economicus), который ведет себя таким образом, чтобы максимизировать свою полезность. Несмотря на всю априорную ограниченность этой теории (потому что не всегда понятно, что такое полезность, почему человек стремиться ее максимизировать), концепция оказалась плодотворной.

Пусть имеется один субъект (агент), который может выбирать действия из какого-то множества. Предположим, что предпочтения этого субъекта описывается функцией полезности 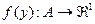(или целевой функцией, функцией предпочтения – будем использовать в настоящем разделе эти термины как синонимы), которая отображает множество его допустимых действий (альтернатив) A на числовую ось Â ¹. Значения этой функции позволяют сравнивать разные альтернативы (действия). Если есть два варианта – два элемента из множества допустимых действий, то лучшим будет тот, который приводит к большему значению функции. Предположим, что агент будет максимизировать свою полезность и производить выбор из множества выбора, которое представляет собой множество максимумов его целевой функции:

(1) .

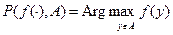Значит, множество выбора агента зависит от его предпочтений f (×) и от того множества A, из которого он производит выбор.

Множество выбора зависит от двух составляющих: от функции и от допустимого множества. Предположение, что агент производит выбор из множества выбора (то есть, стремится максимизировать свою целевую функцию) называется гипотезой рационального поведения, которая заключается в том, что агент выбирает с учетом всей имеющейся у него информации наилучшую с его точки зрения допустимую альтернативу, т.е. одну из альтернатив y^*, на которых достигается максимум его целевой функции:

(2) y^* = arg 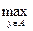f (y).

Пример 2.1. Рассмотрим экономического агента – производственное предприятие – принимающего решение об объеме выпускаемой продукции y. Технология производства такова, что может быть произведен любой объем продукции, не превышающий технологического ограничения y⁺ > 0, то есть множество допустимых действий агента A = [0; y⁺]. Предположим, что известна рыночная цена l > 0 на продукцию, производимую агентом, и известна функция затрат агента c(y) = y² / 2 r, где r > 0 – тип агента (параметр, отражающий эффективность его деятельности).

Если считать, что агент заинтересован в максимизации своей прибыли (разности между выручкой от продаж и затратами), то его функция полезности примет вид:

(3) f (y) = l y – y ² / 2 r.

Максимум этой функции на положительной полуоси достигается при выборе действия y _max = l r. Значит решение задачи (2) имеет вид:

(4) y^* = min{l r, y ⁺},

то есть агенту следует выбирать объем производства, максимизирующий его прибыль (если такой объем является технологически допустимым), либо максимально возможный (с точки зрения технологических ограничений) объем производства. ·

Помимо принципа (1) принятия решений, агент может использовать принципы ограниченной рациональности, то есть выбирать e-оптимальные действия:

(5) P_e (f (×) ,A) = { y Î A | f (y) ³ f (y^*) – e},

или действия, обеспечивающие ему заданный уровень полезности:

(6) P (f (×), A, } = { y Î A | f (y) ³ }.

Пример 2.2. Рассмотрим Пример 2.1, в котором агент готов выбирать e-оптимальные действия, то есть, действия, которые обеспечивают ему прибыль, отличающуюся от максимально возможной не более чем на e. Предполагая, что технологические ограничения отсутствуют (y⁺ = +¥), из (3) и (5) получим:

(7) P _e(f (×), A) = [l r – ; l r + ],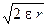

В свою очередь, из (3) и (6) получим:

(8) P (f (×), A, } = [l r – 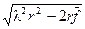; l r + ]

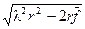Отметим, что при e = 0 или = f (y^*), получаем, что (7) и (8) превращаются в соответствующее целевой функции (3) выражение (1). Последнее свойство называется принципом обобщения – при предельном переходе к случаю, который был обобщен, все результаты должны соответствовать обобщаемым результатам (отметим, что принцип обобщения справедлив в рамках одной научной парадигмы).

Кроме того, интересно отметить, что имеет место принцип монотонности по уровню притязаний – с ростом e (тех потерь, которые агент считает допустимыми) или с уменьшением значения (той полезности, которой агент считает достаточной), множества (7) и (8) расширяются. ·

Альтернативой описанию предпочтений агента в терминах функции полезности является их описание в терминах отношений предпочтения.

Дата добавления: 2014-01-20