Отношения предпочтения

Как отмечалось выше, в основе теории принятия решений лежит предположение, что человек, поставленный перед проблемой выбора, в процессе выработки решения (выбора альтернативы) руководствуется своими предпочтениями, то есть выбирает действие, которое, по его мнению, приведет к наиболее предпочтительному для него результату деятельности (исходу). Формальное описание процесса сравнения альтернатив может быть дано через отношения предпочтения и неразличимости.

Бинарное отношение Ã на множестве A – это подмножество Ã Í A ´ A, где 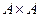– множество всех упорядоченных пар 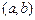, . Если (a, b) Î Ã, говорят, что отношение Ã выполнено (или имеет место) для (a, b) и пишут aÃb.

Если бинарное отношение Ã не имеет места для a, b, этот факт обозначается aÃ^cb.

Отношение предпочтения – это бинарное отношение, определяемое свойством: 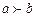тогда и только тогда, когда a предпочтительнее (лучше) для ЛПР, чем b.

Отношение неразличимости 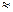имеет место для пары a, b тогда и только тогда, когда 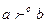и .

Отношение Ã называется рефлексивным, если для всех a Î A выполнено aÃa, антирефлексивным, если для всех a Î A выполнено aÃ^ca.

Отношение Ã называется антисимметричым, если из aÃb и bÃa следует , асимметричным, если из aÃb следует bÃ^ca.

Далее рассматривается отношение строгого предпочтения , для которого выполнено условие асимметричности.

Отношение Ã называется транзитивным, если для всех a, b, c Î A из aÃb и bÃc следует aÃc.

Отношение Ã называется полным, если для всех a, b Î A выполнено aÃb или bÃa.

Пусть на множестве исходов A ₀ задано предпочтение ЛПР, то есть отношение типа 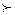, которое для пары a, b исходов из A ₀ выполняется, если a лучше b с точки зрения лица, принимающего решение. Определим также множество действий A. Это множество содержит все возможные действия ЛПР и состоит из элементов вида «Сделать то-то», «Приказать то-то», «Купить то-то…» и пр.

Рассмотрим пример, который иллюстрирует описание предпочтений агента бинарными отношениями (см. также Пример 2.7 ниже).

Пример 2.3. Рассмотрим фирму, принимающую решение о выходе на новый для нее рынок. Пусть она имеет три возможных способа действий: выходить на еще неосвоенный рынок с некоторой принципиально новой продукцией (обозначим это действие через y ₁), выходить на один из «традиционных» рынков (y ₂) или не выходить на новые рынки вовсе (y ₃). То есть множество A возможных действий фирмы состоит из трех элементов: A = { y ₁, y ₂, y ₃}.

Выход на новый рынок (действие y ₁) требует существенных инвестиций в научные исследования и новое производство, характеризуясь, в то же время, потенциально высокими рисками – новая продукция может не найти спроса и фирма разорится. С входом на традиционные рынки (действие y ₂) связана другая проблема – конкуренция. Фирма может не выдержать давления конкурентов, что также приведет к ее разорению. Помимо этого, даже при удачном развитии событий прибыль фирмы в этом случае будет меньше, чем при успешном выходе на новый рынок. «Пассивная» позиция (действие y ₃) характеризуется отсутствием новых прибылей, но и полным отсутствием рисков (сохранение status quo).

Рассмотрим возможные исходы – результаты, к которым может привести то или иное действие фирмы. Пусть в настоящее время прибыли фирмы характеризуются как «низкие». Исход, соответствующий сохранению текущей прибыльности, обозначим через z ₁. Кроме того, будем считать, что возможны еще два значения прибыльности, которые условно назовем «средние прибыли» (соответствующий исход обозначим через z ₂) и «высокие прибыли» (z ₃). Исход, соответствующий разорению фирмы, обозначим через z ₀.

Таким образом, три возможных действия фирмы приводят к четырем возможным исходам, то есть в данном примере множество исходов A ₀ = { z ₀, z ₁, z ₂, z ₃}.

Предпочтения фирмы на множестве исходов задаются строгим упорядочением 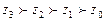. Это бинарное отношение говорит просто о том, что бóльшие прибыли более предпочтительны для фирмы, а наихудшим исходом для нее, очевидно, является разорение (z ₀).

Однако определением множеств A ₀, A и отношения предпочтения на A ₀ формулировка задачи принятия решения не исчерпывается. Необходимо определить еще и связь между принятым решением и реализующимся результатом.

Задача принятия решения – это задача выбора ЛПР действия из множества A, которое приводит к наилучшему с точки зрения предпочтения ЛПР результату из A ₀. Чтобы решить эту задачу, необходимо тем или иным образом из отношения предпочтения на множестве исходов A ₀ вывести отношение предпочтения на множестве действий A, а затем выбрать наиболее предпочтительное действие.

Пусть имеется некоторая функция w: A ® A ₀ – детерминированное (однозначное) соответствие между выбранным действием и его результатом. В этом случае выбор действия равнозначен выбору результата. Задача, таким образом, состоит лишь в нахождении реализуемого исхода (то есть исхода, для которого есть действие, его реализующее), предпочтительного по отношению ко всем остальным реализуемым исходам. Выбранное действие будет принадлежать множеству («аналог» выражения (1) раздела 2.1.1):

(1) P (Ã, A) = .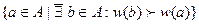

Если бы в рассматриваемом примере с фирмой, выходящей на рынок, функция w (×) была задана следующим образом:

1. w («y ₁) = z ₃,

2. w (y ₂) = z ₂,

3. w (z ₃) = z ₁,

то, очевидно, решением задачи принятия решения было бы действие y ₁ – «выходить на новый рынок», то есть действие, приводящее к наилучшему реализуемому результату z ₃.

Такая задача называется детерминированной задачей принятия решения. Более сложная модель, учитывающая риски принимаемых фирмой решений, описывается ниже (см. Пример 2.6). ·

Возникает вопрос, а как связаны между собой функции полезности и отношения предпочтения? Соответствие между отношением предпочтения и функцией полезности определяется условием

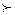(2) f (a) > f (b) Û a b.

Очевидно, что функция полезности порождает полное транзитивное бинарное отношение. Рассмотрим, каким ограничениям должно удовлетворять отношение предпочтения, чтобы можно было рассматривать вместо него функцию полезности. Эта задача является предметом изучения математической теории полезности (впервые вопрос о представимости отношения предпочтения функцией полезности – см. (2) – рассматривался Г. Кантором (1895 г.)).

Как отмечалось выше, отношение предпочтения – бинарное отношение на множестве исходов A ₀, удовлетворяющее, как минимум, свойству асимметрии. Для продуктивного использования, однако, необходимы дополнительные условия на отношение предпочтения. При этом то, какие дополнительные предположения необходимо сделать, чтобы получить инструмент, с которым можно работать, не отходя в то же время от встречающихся в реальной жизни предпочтений – это вопрос, который на протяжении многих лет служил предметом дискуссий и продолжает обсуждаться до сих пор. Дело в том, что подобные дополнительные предположения вводятся в виде аксиом, некоторых гипотез о закономерностях процесса выбора.

Дата добавления: 2014-01-20