Суперпозиция полей

Знание поля точечного заряда позволяет в принципе рассчитывать поля, создаваемые как несколькими зарядами, так и протяженными заряженными телами. Для этого в физике используется простой, но очень важный принцип суперпозиции (наложения) полей, суть которого рассмотрим в данном параграфе.

Пусть имеется система точечных электрических зарядов 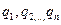. Найдём напряженность электрического поля, создаваемой этими зарядами, в произвольной точке. Мысленно поместим в эту точку пробный заряд 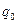. Опытным путём установлено, что сила 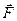, с которой система зарядов действует на этот заряд, равна векторной сумме сил, приложенных к нему со стороны каждого из зарядов :

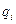или в сокращенной записи

.

Разделим это равенство на заряд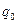

или .

Согласно формуле (2.1) - напряжённость электрических полей, создаваемых отдельными зарядами 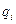в данной точке, а 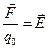- напряжённость электрического поля системы зарядов в той же точке. Поэтому

, (3.1)

т.е. напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создаёт каждый заряд системы в отдельности. Соотношение (3.1) называют принципом суперпозиции полей.

Пусть поле в точке А создано тремя полями, с напряженностями в этой точке 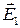, , 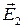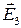(рис. 3.1). Воспользуемся принципом супепозиции и найдем результирующее значение напяженности. Для геометрического сложения используем правилом многоугольника: последовательно соединяем, параллельно перенося, все вектора, так, что к концу предыдущего вектора присоединяется начало последующего (рис. 3.2), и вектор соединяющий начало первого и конец последнего есть резельтат сложения. В нашем случае - результирующее значение вектора напряженности.

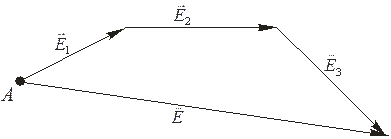Рис. 3.1 Рис. 3.2

Для нахождения напряжённости электростатического поля, создаваемого заряженным протяжённым телом в некоторой точке, тело мысленно разбивают на элементарные части с зарядом , которые можно принять за точечные заряды. Тогда элементарную напряжённость 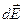в этой точке находим по формуле (2.2) . Используя принцип суперпозиции полей, напряжённость поля 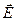в данной точке будет равна:

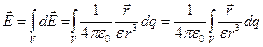, (3.2)

где 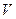— объём тела, поскольку суммирование элементарных величин означает интегрирование.

Дата добавления: 2014-01-20