Поле бесконечного заряженного цилиндра

Пусть поле создается бесконечной цилиндрической поверхностью радиуса 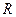, заряженной с постоянной поверхностной плотностью 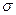(заряд предполагаем положительным.). Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть только от расстояния 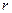от оси цилиндра. Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса 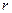и высоты 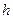(рис. 7.6). Для снований цилиндра 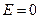, для боковой поверхности напряженность зависит от радиуса 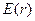. Следовательно, поток вектора 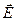через рассматриваемую поверхность равен 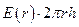. Если 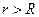, внутрь поверхности попадает заряд 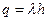, где 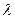- линейная плотность заряда. Применив теорему Гаусса, получим

.

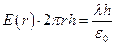Следовательно

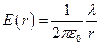
. (7.3)

Если , рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего .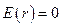

(Рис. 7.6)(Савельев стр. 57, 14.5)

Таким образом, внутри равномерно заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда 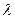и расстоянием 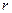от оси цилиндра.

Поле отрицательно заряженного цилиндра отличается от поля цилиндра, заряженного положительно, только направлением вектора напряженности .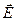

Из формулы (7.3) следует, что, уменьшая радиус цилиндра 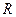(при неизменной линейной плотности заряда 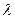), можно получить вблизи поверхности цилиндра поле с очень большой напряженностью.

Подставив в (7.3) 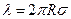и положив 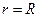, получим для напряженности поля в непосредственной близости к поверхности цилиндра значение

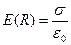. (7.4)

С помощью принципа суперпозиции легко найти поле двух коаксиальных цилиндрических поверхностей, заряженных одинаковой по величине, но отличающейся знаком линейной плотность 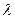(рис. 7.7). Внутри меньшего и вне большого цилиндров поле отсутствует. В зазоре между цилиндрами величина напряженности поля определяется формулой (7.3). Это справедливо и для цилиндрических поверхностей конечной длины, если зазор межу поверхностями много меньше их длины (цилиндрический конденсатор). Заметные отступления от поля поверхностей бесконечной длины будут наблюдаться только вблизи краев цилиндров.

(Рис. 7.7)(Савельев стр. 58, 14.6)

Дата добавления: 2014-01-20