
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Потенциал и разность потенциалов электростатического поля
|
|
|
|
Наряду с напряжённостью, для характеристики электростатического поля вводят ещё одну физическую величину, называемую потенциалом, которая является энергетической характеристикой этого поля. Заряды, помещённые в электростатическое поле, обладают потенциальными энергиями. Если в одну и ту же точку поля вносить различные пробные заряды 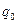 , то они будут обладать различной потенциальной энергией
, то они будут обладать различной потенциальной энергией 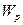 относительно некоторого нулевого уровня. Однако отношение
относительно некоторого нулевого уровня. Однако отношение  для всех зарядов будет оставаться одинаковым независимо от их величины. Поэтому его принимают за характеристику поля в данной точке. Обозначим это отношение через
для всех зарядов будет оставаться одинаковым независимо от их величины. Поэтому его принимают за характеристику поля в данной точке. Обозначим это отношение через 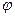 . Тогда
. Тогда
 , (9.1)
, (9.1)
т.е. потенциалом электростатического поля называется отношение потенциальной энергии, которой обладает заряд в некоторой точке поля, к величине этого заряда.
Из механики известно, что работа перемещения тела из одной точки потенциального поля в другую равна уменьшению его потенциальной энергии. Поэтому работа  по переносу заряда
по переносу заряда 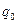 из точки 1 в точку 2 будет равна:
из точки 1 в точку 2 будет равна:
 , (9.2)
, (9.2)
где 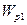 и
и  - потенциальная энергия заряда в этих точках. Из (9.1) следует
- потенциальная энергия заряда в этих точках. Из (9.1) следует  и
и  , где
, где 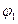 и
и  - потенциалы поля в указанных точках. С учётом этого из (9.2) получаем
- потенциалы поля в указанных точках. С учётом этого из (9.2) получаем
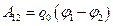 . (9.3)
. (9.3)
Отсюда
 , (9.4)
, (9.4)
т.е. разностью потенциалов электростатического поля называется отношение работы, совершаемой силами поля при перемещении заряда из одной точки поля в другую, к величине этого заряда.
Из формулы (9.4) можно дать и иное определение потенциала. Пусть заряд 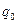 переносится из произвольной точки поля с потенциалом
переносится из произвольной точки поля с потенциалом 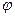 в бесконечность, где потенциал условно принимается за ноль, так как электростатическое поле на большом расстоянии от зарядов, создающих поле, практически отсутствует, т.е.
в бесконечность, где потенциал условно принимается за ноль, так как электростатическое поле на большом расстоянии от зарядов, создающих поле, практически отсутствует, т.е. 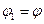 и
и 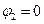 . Тогда
. Тогда
 , (9.5)
, (9.5)
т.е. потенциал равен отношению работы, которую совершают силы электростатического поля при перемещении пробного заряда из данной точки в бесконечность, к величине этого заряда.
В системе единиц СИ разность потенциалов измеряется в вольтах (B).
1 В = 1 Дж/1 Кл, т.е. 1 В — разность потенциалов между двумя точками, при
переносе между которыми заряда в 1 Кл совершается работа 1 Дж.
В случае поля, создаваемого точечным зарядом, согласно формулам (8.1) и (9.2), получаем:  и
и  . Отсюда
. Отсюда  и
и 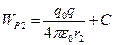 . В данном случае выражения потенциальных энергий содержат некоторую константу
. В данном случае выражения потенциальных энергий содержат некоторую константу 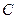 , поскольку в общем случае потенциальная энергия определяется только с точностью до постоянной величины. При подстановке этих выражений в формулу (9.2) постоянная величина
, поскольку в общем случае потенциальная энергия определяется только с точностью до постоянной величины. При подстановке этих выражений в формулу (9.2) постоянная величина 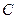 взаимно уничтожается. Таким образом, потенциальная энергия заряда
взаимно уничтожается. Таким образом, потенциальная энергия заряда 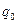 , находящегося в электростатическом поле точечного заряда
, находящегося в электростатическом поле точечного заряда 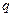 , записывается в виде
, записывается в виде
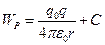 .
.
Величина 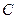 выбирается таким образом, чтобы при удалении заряда на бесконечность
выбирается таким образом, чтобы при удалении заряда на бесконечность  потенциальная энергия обращалась бы в ноль, т.е.
потенциальная энергия обращалась бы в ноль, т.е.  . Тогда
. Тогда  и
и
 . (9.6)
. (9.6)
Подставляя это выражение в (9.1), получаем формулу, по которой рассчитывают потенциал в различных точках электростатического поля точечного заряда:
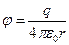 . (9.7)
. (9.7)
Если поле создано несколькими полями, то для расчета потенциала можно воспользоваться принципом суперпозиции:
 , (9.8)
, (9.8)
т.е. потенциал поля созданного системой зарядов, равен алгебраической сумме потенциалов полей, созданного каждым зарядом в отдельности. Знак потенциала совпадает со знаком заряда 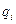 отдельных зарядов системы.
отдельных зарядов системы.
Если поле создано заряженной сферической поверхностью, то потенциал можно рассчитать с помощью следующего выражения
 , (9.9)
, (9.9)
где 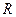 - радиус сферы.
- радиус сферы.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 418; Нарушение авторских прав?; Мы поможем в написании вашей работы!