Диполь. Поле диполя

Электрическая система, состоящая из двух равных по абсолютной величине и противоположных по знаку точечных зарядов, отстоящих друг от друга на расстоянии, много меньшем, чем расстояние до рассматриваемых точек поля, называется электрическим диполем. Диполь характеризуется двумя величинами – это плечо диполя и дипольный момент (рис. 5.1). Плечо диполя 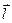- вектор, направленный от отрицательного заряда к положительному, равный по длине расстоянию между зарядами 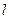. Дипольный момент 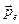является вектором, направленным от отрицательного заряда к положительному заряду, равный произведению плеча диполя на положительный заряд

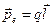. (12.1)

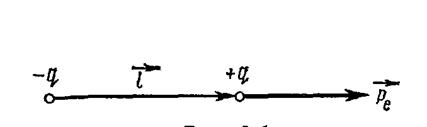РИС 12.1

рис 12.2

Рассчитаем поле в точке А, расположенной на оси диполя, т.е. на прямой проходящей через заряды (рис. 12.2). В соответствии с принципом суперпозиции полей напряженность в произвольной точке поля диполя

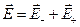, (12.2)

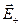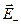где и — напряженности полей зарядов 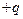и 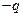. Векторы 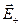и 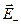направлены также вдоль этой оси, но в противоположные стороны. По формуле (2.2),

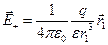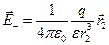, , (12.3)

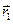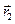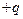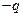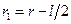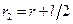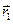где и — радиусы-векторы, проведенные в точку А из концов диполя и , причем и ; и 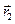совпадают по направлению с вектором 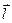, поэтому

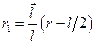и 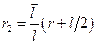. (12.4)

Подставим выражения (12.4) в (12.3)

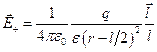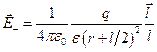, , (12.5)

Учитывая (12.5), выражение (12.2) примет вид

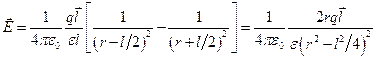. (12.6)

Учитывая, что 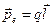, получим

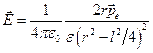. (12.7)

Если 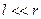, то членом 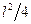по сравнению с 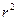можно пренебречь. Тогда

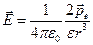; (12.8)

численное значение напряженности

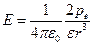. (12.9)

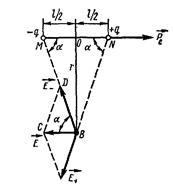Рис. 12.3

Найдем напряженность поля диполя в точке В, расположенной на перпендикуляре, восставленном к оси диполя из его середины О (рис. 12.3). Точка В равноудалена от зарядов 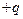и 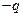. Поэтому

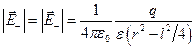. (12.10)

Треугольники BMN и BCD — равнобедренные, причем углы при вершинах М и N 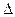BMN и при вершинах В и С 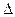BCD одинаковы и равны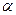. Так как стороны ВМ и BD, а также BN и DC попарно параллельны, то стороны MN и ВС параллельны, т.е. вектор 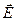противоположен по направлению электрическому моменту диполя :

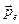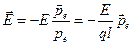. (12.11)

Из рис. 2.3 видно, что числовое значение напряженности поля в точке В равно

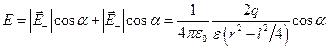. (12.12)

Из 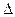ВМО имеем . Поэтому

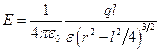. (12.13)

Пренебрегая величиной 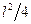по сравнению с 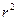, получим

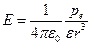. (12.14)

Из (12.11) и (12.14) следует, что вектор напряженности поля в точке В равен

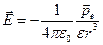. (12.15)

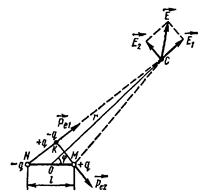Рис. 12.4

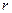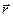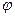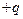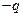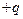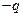Рассмотрим теперь общий случай. Пусть точка С лежит на расстоянии от середины О диполя, причем радиус-вектор образует с осью диполя угол (рис. 12.4). Соединим пунктиром заряды и с точкой С и опустим на прямую NC перпендикуляр да точки М. Поместим в основании К этого перпендикуляра два точечных заряда и . Расположенные в одной и той же точке равные по величине и противоположные по знаку заряды 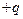и 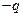полностью нейтрализуют друг друга и не искажают поля диполя. Четыре заряда, находящиеся в точках М, N и К, можно рассматривать как два диполя (NK и МК). Ввиду малости расстояния 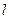по сравнению с 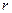угол CNM 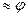. Поэтому электрические моменты первого и второго диполей соответственно равны:

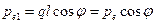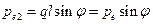, . (12.16)

Для первого диполя точка С лежит на его оси, а для второго — на перпендикуляре, восставленном в средней точке оси. По формулам (12.8) и (12.15) напряженност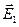и и 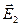полей, создаваемых в точке С каждым из диполей, равны

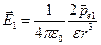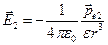, . (12.17)

Векторы 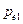и 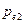и соответственно 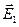и 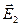взаимно перпендикулярны. Поэтому численное значение напряженности поля диполя MN в точке С моменты первого и второго диполей соответственно

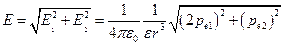. (12.18)

Подставив сюда значения 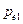и 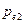из (12.16), получим

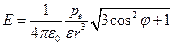. (12.19)

Формула (12.19) охватывает все возможные случаи расположения точки С. При 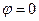она совпадает с (12.9), а при 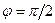— с (12.14).

Дата добавления: 2014-01-20