Вектор поляризации

Количественной мерой поляризации диэлектрика служит вектор поляризации 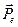. Вектором поляризации или поляризованностью называют отношение дипольного электрического момента малого объема 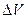диэлектрика к этому объему:

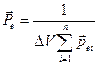, (13.1)

где 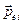— дипольный момент 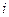-й молекулы, 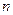— общее число молекул в объеме 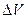. Этот объем должен быть столь малым, чтобы в его пределах электрическое поле можно было считать однородным. В то же время в нем должно содержаться еще столь большое число молекул диэлектрика (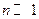), чтобы к ним можно было применять статистические методы исследования.

В Международной системе единиц (СИ) вектор поляризации выражается в кулонах на квадратный метр ().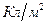

В случае однородного диэлектрика с неполярными молекулами, находящегося в электрическом поле,

, (13.2)

где 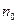— концентрация молекул, т. е. их число в единице объема. Это следует из того, что векторы 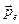всех молекул имеют одинаковое направление — вдоль напряженности 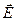поля в диэлектрике. Используя формулу (12.7), получим

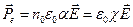. (13.3)

Коэффициент

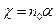(13.4)

называется диэлектрической восприимчивостью вещества. Данная величина связана с диэлектрической проницаемостью следующим соотношением:

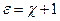. (13.5)

П. Дебай показал, что в случае слабых электрических полей формула (13.3) справедлива также для диэлектриков с полярными молекулами. Диэлектрическая восприимчивость такого диэлектрика в слабых полях выражается формулой

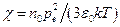, (13.6)

где 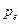— постоянный электрический дипольный момент молекулы, 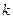- постоянная Больцмана, 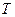— абсолютная температура.

При увеличении напряженности электрического поля или понижении температуры линейная зависимость 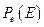для диэлектриков с полярными молекулами нарушается (рис. 13.1). С увеличением 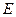достигается такое состояние, когда дипольные моменты практически всех молекул направлены вдоль поля. Дальнейшее усиление поля уже не может вызывать увеличения 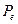, так как наступает «насыщение» (горизонтальная часть кривой на рис. 13.1), характеризуемое постоянной величиной .

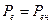Рис. 13.1

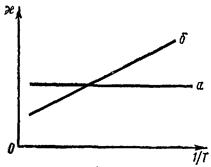Рис. 13.2

На рис. 13.2 представлена зависимость диэлектрической восприимчивости 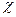от 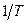в случае неполярных (а) и полярных (б) молекул. Как уже указывалось, в полярных молекулах наблюдается не только ориентационная, но и электронная поляризация. Поэтому прямая б, показывающая уменьшение диэлектрической восприимчивости при нагревании диэлектрика с полярными молекулами, не проходит через начало координат.

Фактически в этом случае 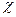состоит из двух частей:

,

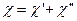где 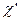и 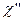выражаются соответственно формулами (13.4) и (13.6).

Вектор поляризации совпадает по направлению с вектором напряженности поля и связан с ним соотношением (13.3) только в электрически изотропной среде. Диэлектрическая восприимчивость анизотропной среды (например, кристаллической) — величина тензорная. Ее значение различно вдоль разных направлений. В такой среде связь между векторам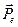и и 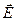имеет вид более сложный, чем (13.3):

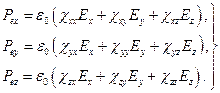(13.7)

Значения 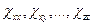зависят не только от природы и состояния электрически анизотропной среды, но и от ориентации осей координат 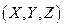по отношению к характерным для этой среды направлениям (ее кристаллографическим осям). Из (13.7) видно, что в общем случае в анизотропной среде проекции векторов 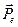и 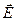на оси координат не пропорциональны друг другу, а потому и сами векторы 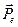и 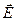неколлинеарны. В дальнейшем мы будем рассматривать только электрически изотропные диэлектрики.

Дата добавления: 2014-01-20