Сегнетоэлектрики. 10 страница

следует, что при всяком изменении магнитного потока, пронизывающего площадь, охватываемую проводником, в нём возникает ЭДС индукции, под действием которой в проводнике появляется индукционный ток, если проводник замкнутый. Однако ЭДС в любой цепи возникает лишь в том случае, когда в ней на носители тока действуют сторонние силы, т.е. силы не электростатического происхождения. Поэтому правомерен вопрос о природе сторонних сил, создающих ЭДС индукции.

Для объяснения ЭДС индукции Максвелл выдвинул гипотезу, что переменное магнитное поле создаёт в окружающем пространстве электрическое поле. Силовые линии магнитного поля концентрически охвачены силовыми линиями электрического поля (рис. 49.1). Такое электрическое поле — с замкнутыми силовыми линиями — называется вихревым полем. Это поле действует на свободные заряды проводника, приводя их в упорядоченное движение, т.е. создавая индукционный ток.

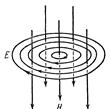Рис. 49.1

По Максвеллу, изменяющееся во времени магнитное поле порождает электрическое поле 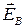, циркуляция которого равна

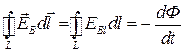, (49.1)

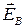где — проекция вектора на направление .

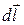Подставив в формулу (49.1) выражение

,

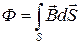получим

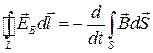. (49.2)

Если поверхность и контур неподвижны, то операции дифференцирования и интегрирования можно поменять местами. Следовательно,

, (49.3)

где символ частной производной подчеркивает тот факт, что интеграл является функцией только времени.

Выражение (49.3) одно из уравнений Максвелла, говорящее о том, что элекрическое поле порожается магнитным.

Второе предположение, высказанное Максвеллом – это то, что переменное электрическое поле вызывает возникновение магнитного поля. Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, одержащую конденсатор (рис. 49.2). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники.

По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (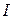) и смещения (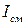) равны:

.

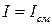Ток проводимости вблизи обкладок конденсатора

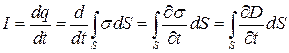, (49.4)

(поверхностная плотность заряда 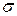на обкладках равна электрическому смещению D в конденсаторе). В общем случае индукция электрического поля может зависеть от координат и времени. Поэтому в выражении (49.4) производную 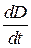мы заменили частной производной 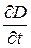по времени. Подынтегральное выражение в (49.4) можно рассматривать как частный случай скалярного произведения 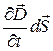, когда 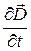и 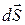взаимно параллельны. Поэтому для общего случая можно записать

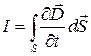. (49.5)

Сравнивая это выражение с 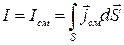, имеем

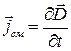. (49.6)

Выражение (49.6) было названо Максвеллом плотностью тока смещения.

Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Следует отметить, что название «ток смещения» является условным, а точнее исторически сложившимся, так как ток смещения по своей сути — это изменяющееся со временем электрическое поле. Ток смещения, поэтому, существует не только в вакууме но и внутри проводников, по которым проходит переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с током проводимости. На основании этого Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока

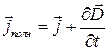. (49.7)

Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т.е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Используя формулу (49.7) можно получит обобщенную теорему о циркулции вектора

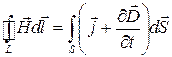. (49.8)

Выражение (49.8) это еще одно из уравнений Максвелла, из которого видно, что источниками магнитного поля могут быть либо движущиеся заряды (электрические токи) 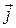, либо переменные электрические поля .

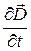Третьим уравнением, вошедшим в систему уравнений Гаусса, является теорема Гаусса для поля электрического поля:

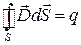. (49.9)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (49.9) запишется в виде

. (49.10)

Данное уравнение утверждает, что электрическое поле создается электрическими зарядами.

Еще одним уравнением Максвелла является теорема Гаусса для магнитного поля

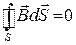, (49.11)

сообщающее о том, что в природе не существует магнитных зарядов.

Полная система уравнений Максвелла в интегральной форме:

,

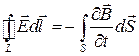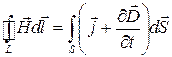, (49.12)

,

.

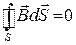Эти уравнения, лежащие в основе электромагнетизма, можно дополнить выражениями, связывающими величины, входящие в уравнения

,

,

.

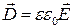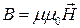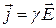Рассмотрим, какой вид примут уравнения Максвелла для стационарных электрического 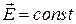и магнитного 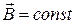полей. В первом уравнении диферениал 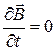, следовательно оно принемает вид

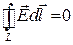. (49.13)

Во втором уравнении 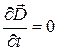, следовательно уравнение запишется так

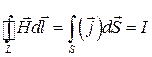, (49.14)

Выражение рационально записать в форме (49.9). Последнее уравнеие останется без изменения. Система уравнений Максвелла для стационарных полей:

,

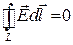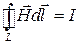, (49.15)

,

.

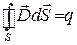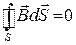Из системы (49.15) видно, что источниками электрического поля в являются только электрические заряды, а источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользуемся известными из векторного анализа теоремами Стокса и Гаусса

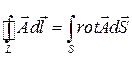, (49.16)

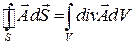, (49.17)

здесь 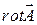- ротор (вихрь) вектора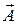

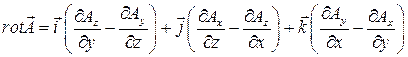, (49.18)

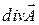- дивергенция (расхождение) вектора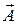

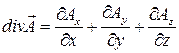. (49.19)

Представим полную систему уравнений Максвелла в дифференциальной форме:

,

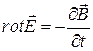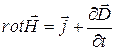, (49.20)

,

.

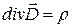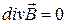Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Дата добавления: 2014-01-20