
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В кривошипно-коромысловом механизме кривошип – самое короткое звено
|
|
|
|
Выполнение этих 2-х условий гарантирует проворачиваемость механизма, т.е. возможность поворота кривошипа на 360°.
3.4. Критерий положений ведомого звена
Смысл критерия заключается в определении соотношений между длинами звеньев, при которых обеспечиваются заданные положения выходных звеньев (в данном случае заданные крайние положения).
Ориентируясь на схемы заданий к курсовому проекту, рассмотрим примеры расчета длин звеньев применительно к кривошипно-коромысловому и коромыслово-ползунному механизмам. Оба механизма являются частями главного исполнительного механизма качающегося конвейера.
Пример 1
 Дано: Кривошипно-коромысловый механизм (Рис.3.6); выходное звено – коромысло СВ; заданы размеры СВ=R, yл , yп, ОС=L.
Дано: Кривошипно-коромысловый механизм (Рис.3.6); выходное звено – коромысло СВ; заданы размеры СВ=R, yл , yп, ОС=L.
Определить: длины звеньев ОА = r, АВ = l, обеспечивающие углы yл , yп в крайних положениях коромысла СВ.
Рис. 3.6
Решение.
Рассмотрим механизм в крайних положениях (Рис.3.6).
Применив теорему косинусов, получим:
Для 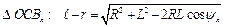 (3.7)
(3.7)
Для 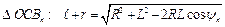 (3.8)
(3.8)
Сложим почленно (3.7) + (3.8) и решим равенство относительно l:
 (3.9)
(3.9)
Вычтем почленно (3.8) - (3.7) и решим равенство относительно 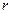 :
:
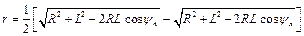 (3.10)
(3.10)
Система 2-х уравнений (3.7) - (3.8) содержит 6 независимых геометрических параметров. Это значит, что можно найти 2 любых параметра, если остальные 4 заданы (причем в любых комбинациях).
Так, например, в курсовом проекте:
задаются - r, L, yл, yп, а подлежат определению - l, R.
Пример 2
 Дано: Коромыслово-ползунный механизм (Рис.3.7); выходное звено – ползун; заданы размеры jл = jп = j, S.
Дано: Коромыслово-ползунный механизм (Рис.3.7); выходное звено – ползун; заданы размеры jл = jп = j, S.
Определить: длину звена СВ = R, обеспечивающую перемещение ползуна на расстояние S.
Решение.
Из рис.3.7 следует:
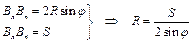 (3.11)
(3.11)
Заметим, что выражение (3.11) справедливо для произвольного значения lВD.
3.5. Критерий максимального угла давления
На рис.3.8 изображена кинематическая пара, образованная шатуном 1 (ведущее звено) и ползуном 2 (ведомое звено).
Угол давления в кинематической паре шатун-ползун – это угол 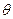 между направлением скорости ползуна
между направлением скорости ползуна 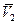 и направлением силы давления шатуна на ползун. Известно, что (при невесомом шатуне) эта сила давления будет направлена вдоль шатуна (если шатун криволинейный – то по прямой, соединяющей концевые шарниры звена).
и направлением силы давления шатуна на ползун. Известно, что (при невесомом шатуне) эта сила давления будет направлена вдоль шатуна (если шатун криволинейный – то по прямой, соединяющей концевые шарниры звена).
 Угол давления имеет большое значение для работоспособности механизма и его КПД. Большие углы давления приводят к повышенной силе трения между ползуном и направляющей стойки. Это влияет на равномерность движения механизма, степень износа подшипников, а иногда приводит к полной остановке механизма вследствие заклинивания.
Угол давления имеет большое значение для работоспособности механизма и его КПД. Большие углы давления приводят к повышенной силе трения между ползуном и направляющей стойки. Это влияет на равномерность движения механизма, степень износа подшипников, а иногда приводит к полной остановке механизма вследствие заклинивания.
Рис.3.8
 На рис.3.9 изображен ползун, входящий в кинематические пары с шатуном и стойкой. Сила
На рис.3.9 изображен ползун, входящий в кинематические пары с шатуном и стойкой. Сила 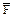 давления шатуна на ползун, разложена на составляющие
давления шатуна на ползун, разложена на составляющие 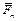 и
и  . Касательная составляющая
. Касательная составляющая 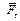 обеспечивает перемещение ползуна вдоль стойки и совершает положительную работу, т.е. является полезной движущей силой. Нормальная составляющая
обеспечивает перемещение ползуна вдоль стойки и совершает положительную работу, т.е. является полезной движущей силой. Нормальная составляющая 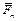 , направленная перпендикулярно, работу по перемещению ползуна не совершает. Напротив, именно эта сила нормального давления определяет величину силы трения между ползуном и стойкой.
, направленная перпендикулярно, работу по перемещению ползуна не совершает. Напротив, именно эта сила нормального давления определяет величину силы трения между ползуном и стойкой.
Действительно, из условия равновесия сил в направлении нормали к направляющей получаем нормальную реакцию стойки 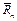 = -
= -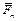 . Далее, на основании закона Кулона, имеем
. Далее, на основании закона Кулона, имеем 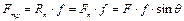 . А отсюда следует, что с увеличением
. А отсюда следует, что с увеличением 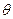 возрастает
возрастает 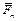 , а вместе с ней и
, а вместе с ней и 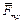 .
.
Следует иметь ввиду, что угол давления 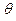 - не постоянная величина, а изменяется в зависимости от положений механизма.
- не постоянная величина, а изменяется в зависимости от положений механизма.
Угол давления 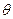 можно уменьшить, если увеличить размеры соответствующих звеньев механизма. При этом габаритные размеры самого механизма увеличиваются, что не всегда приемлемо.
можно уменьшить, если увеличить размеры соответствующих звеньев механизма. При этом габаритные размеры самого механизма увеличиваются, что не всегда приемлемо.
Таким образом, оптимальным вариантом метрического синтеза является тот, когда угол давления в наиболее неблагоприятных положениях механизма достигает максимально допустимого значения, но не превышает его. При создании новых механизмов максимальный угол давления в паре шатун-ползун рекомендуется принимать равным qmax = 30¸40°.
Покажем на примере, как определяется длина звена по критерию «угол давления».
Пример.
 На рис.3.10 изображен кривошипно-ползунный механизм с направляющей, смещенной относительно центра вращения кривошипа на величину эксцентриситета - е*. Заданы длина кривошипа ОА и максимальный угол давления в паре шатун-ползун - qmax.
На рис.3.10 изображен кривошипно-ползунный механизм с направляющей, смещенной относительно центра вращения кривошипа на величину эксцентриситета - е*. Заданы длина кривошипа ОА и максимальный угол давления в паре шатун-ползун - qmax.
Дано: ОА= r, qmax, е*.
Определить: длину шатуна l, из условия, что при полном обороте кривошипа угол давления q не превысит qmax.
Решение.
Рассмотрим изменение угла давления в паре шатун-ползун при прямом и обратном движении ползуна. На рисунке сделаны обозначения:
 - угол давления при прямом ходе;
- угол давления при прямом ходе;
 - угол давления при обратном ходе.
- угол давления при обратном ходе.
Из геометрии следует:
 (3.12)
(3.12) 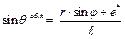 (3.13)
(3.13)
Анализируя (3.12) и (3.13), находим положения механизма, при которых значения углов давления максимальны:
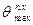 и
и  при
при  (т.е. ОА - вертикально).
(т.е. ОА - вертикально).
Значит:
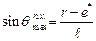 (3.14)
(3.14)  (3.15)
(3.15)
Учитывая, что 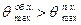 принимаем
принимаем 
Поэтому окончательно:  (3.16)
(3.16)
3.6. Критерий отношения средних скоростей ведомого звена
Иногда при проектировании механизмов бывает важно, чтобы выходное звено на рабочем и на холостом ходу двигалось с различными средними скоростями.[20] В этом случае метрический синтез механизма выполняется с учетом коэффициента отношения средних скоростей.
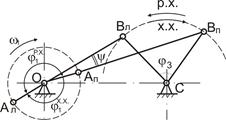 Рассмотрим работу кривошипно-коромыслового механизма (рис. 3.11).
Рассмотрим работу кривошипно-коромыслового механизма (рис. 3.11).
Стрелками на рисунке обозначены:
р.х.– рабочий ход ведомого звена (совершается полезная работа);
х.х. – холостой ход (полезная работа не совершается).
Предположим, что ведущее звено ОА вращается равномерно (w1=const).
Рис.3.11
Из рис. 3.11 видно, что 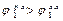 , т.е.
, т.е. 
Коэффициент отношения средних скоростей ведомого звена:
 (для реальных механизмов, типа конвейеров s = 1.1 …1.3)
(для реальных механизмов, типа конвейеров s = 1.1 …1.3)
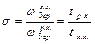 . Это следует из соотношения
. Это следует из соотношения 
Для ведущего звена 
Отсюда
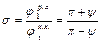
Имея требуемое значение 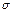 , находят угол
, находят угол 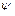 , после чего на основании рис.3.11 определяют необходимые длины звеньев.
, после чего на основании рис.3.11 определяют необходимые длины звеньев.
3.7. Метрический синтез сложного механизма
Сложным механизмом условно будем называть механизм, в состав которого входят несколько структурных групп.
Пример такого механизма показан на рис.3.12. Структурно он состоит из первичного механизма и двух последовательно присоединенных к нему структурных групп.
 Как и в случае простых механизмов, метрический синтез сложного механизма осуществляется с использованием рассмотренных выше или иных критериев. При этом вначале сложный механизм разбивается на более простые механизмы в соответствии с формулой строения. В нашем случае это механизмы ОАВС и СВД.
Как и в случае простых механизмов, метрический синтез сложного механизма осуществляется с использованием рассмотренных выше или иных критериев. При этом вначале сложный механизм разбивается на более простые механизмы в соответствии с формулой строения. В нашем случае это механизмы ОАВС и СВД.
Метрический синтез сложного механизма выполняют в последовательности:
1) синтез первого простого механизма;
2) синтез второго простого механизма;
3) и т.д.
Для закрепления изложенного материала, рассмотрим последовательность операций по метрическому синтезу механизма качающегося конвейера из курсового проекта по ТММ. Предположим, что принципиальная схема механизма задана и изображена на рис.3.13.
Решение:

1. Выделяем простые механизмы: ОАВС и СДЕ.
2. Используем критерий положений коромысла СВ.
Дано:  .
.
3. Используем критерий положений ползуна Е.
Дано: 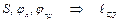 .
.
4. Критерий максимального угла давления в кинематической паре Е - 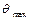 .
.
Дано: 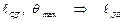 .
.
5. Критерий отношения средних скоростей выходного звена
Дано: крайние положения механизма, угол 
Þ направление вращения ведущего звена.
Вопросы для самоконтроля
1. Какие механизмы в ТММ называют плоскими?
2. Нарисуйте несколько принципиальных схем плоских механизмов. Покажите низшие и высшие кинематические пары, использованные в них.
3. Укажите достоинства и недостатки низших и высших кинематических пар.
4. Объясните смысл задачи структурного синтеза механизма. Что при этом задается, а что подлежит определению?
5. Объясните смысл задачи метрического синтеза механизма. Что при этом задается, а что подлежит определению?
Лекция 4
кинематический анализ плоских рычажных механизмов (графический метод)
4.1. Основная задача и цели кинематического анализа. Методы решения. ([1], §14, п.1; §15, п.1; [2], §3.2; [3], Глава 2, §4)
4.2. Определение положений механизма. ([1], §17; [2], §3.2; [3], Глава 2, §4)
4.3. Определение скоростей точек и угловых скоростей звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)
4.4. Определение ускорений точек и угловых ускорений звеньев механизма. ([1], §18; [2], §3.2; [3], Глава 2, §4)
4.5. Кинематический анализ сложных механизмов ([3], Глава 2, §4).
4.1. Основная задача и цели кинематического анализа. Методы решения.
Основная задача кинематики механизмов – изучение движения точек и звеньев механизма без учета сил, действующих на этот механизм.
Кинематическое исследование механизма преследует три основных цели:
1. Изучение положений механизма. Изучение перемещений точек и углов поворота звеньев ( ). Определение траекторий движения точек.
). Определение траекторий движения точек.
· Результаты исследований по данному пункту используются при определении габаритных размеров механизма, определении формы и размеров внутрикорпусного пространства, определения скоростей, ускорений, решении задач динамического синтеза и анализа.
2. Определение скоростей точек и угловых скоростей звеньев ( ).
).
· Найденные линейные скорости могут быть использованы, в том числе, для определения мощностей сил и приведенной силы; угловые скорости – для определения нормальных ускорений точек, мощностей моментов сил и др. целей.
3. Определение ускорений точек и угловых ускорений звеньев ( ).
).
· Ускорения в задачах динамики позволяют выполнить силовой расчет механизма, т.е. расчет движущей силы и нагруженности кинетических пар по методу кинетостатики (с использованием принципа Даламбера). В кулачковых механизмах по ускорениям судят о динамических нагрузках, возникающих в процессе работы механизма.
Методы кинематического анализа.
1. Графический (преимущества - наглядность, прогнозируемость результатов; недостатки - низкая точность, трудоемкость).
2. Аналитический (высокая точность, но отсутствие наглядности, необходимость дополнительной работы по составлению и отладке программы).
Аналитическое решение удобно на хорошо отлаженных задачах, требующих исследования выходных параметров механизма при различных вариантах исходных данных или оптимизации этих исходных данных.
Кинематическому исследованию механизма, как правило, предшествует структурный анализ, в ходе которого определяется степень подвижности механизма и его класс.
Если механизм имеет степень подвижности, равную единице, то положения, скорости и ускорения точек и звеньев механизма - есть функции положения, скорости и ускорения его начального звена. За начальное звено, обычно, принимают входное звено механизма, а за обобщенную координату – функцию положения этого звена.
Если механизм имеет второй класс, это значит, что он построен на основе простых диад. В этом случае положения точек и звеньев механизма, их скорости и ускорения определяются обычными методами кинематики.
Последующие разделы кинематического анализа (см. пп.4.2 - 4.4) изложены в предположении, что механизм имеет степень подвижности, равную единице, и второй класс по классификации Л.В.Ассура.
4.2. Определение положений механизма (построение планов положений).
Построение планов положений является обязательным этапом при решении задачи кинематического анализа графическим методом. Только планы положений позволяют определить траектории отдельных точек механизма. Только с их помощью можно строить планы скоростей и планы ускорений, определять угловые скорости и угловые ускорения звеньев, выполнять динамические расчеты.
Для лучшего усвоения материала вопрос о построении планов положений рассмотрим системно, выделив исходные данные, цель и порядок решения задачи.
Постановка задачи:
Дано:
- Кинематическая схема механизма (принципиальная схема, построенная в масштабе).
- Положение входного звена или несколько его возможных положений.
Определить:
- Крайние положения механизма.
- Положение звеньев механизма при заданных положениях входного звена.
Порядок решения задачи:
1. Изображение принадлежащих стойке шарниров, направляющих и т.п.
2. Определение крайних положений механизма.
Крайним положением механизма считают такое положение, при котором хотя бы одно звено механизма занимает крайнее положение [4]. При этом под крайним положением звена понимают то его положение, из которого оно может двигаться только в одном направлении. Путь звена, пройденный от одного крайнего положения до другого и измеренный в линейных или угловых единицах измерения, называют ходом звена.
Крайние положения механизмов, входным звеном которых является кривошип, находят по известным правилам:
Правило 1: в кривошипно-коромысловом (Рис.4.1) и кривошипно-ползунном механизмах в крайних положениях кривошип ОА и шатун АВ находятся на одной прямой (ОА || СВ).

Используя это правило, покажем алгоритм построений для механизма (Рис.4.1):
· точки О и С;
· окружность r = ОА;
· окружность R = СВ;
· дуги ОВл = АВ - ОА;
ОВп = АВ + ОА
· точки Вл, Вп, Ал, Ап
Рис.4.1
 Правило 2: в кривошипно-кулисном механизме (Рис.4.2) в крайних положениях кривошип ОА перпендикулярен кулисе СВ (ОА ^ СВ).
Правило 2: в кривошипно-кулисном механизме (Рис.4.2) в крайних положениях кривошип ОА перпендикулярен кулисе СВ (ОА ^ СВ).
Используя это правило, покажем алгоритм построений для механизма (Рис.4.2):
· точки О и С;
· окружность r = ОА;
· касательные из точки С к окружности радиусом r = ОА ® т. Ал , т. Ап;
· ОАл , ОАп - положения кривошипа при крайних положениях кулисы
3. Выбор «нулевого» (начального) положения (обычно одно из крайних положений, соответствующее началу рабочего хода) и направления движения кривошипа.
4. Построение промежуточных положений механизма для заданных положений входного звена (кривошипа) методом засечек.
4.3. Определение скоростей точек (построение планов скоростей) и угловых скоростей звеньев механизма
Построение планов скоростей – важнейшая составляющая кинематического анализа.
Часто на вопрос: «- Зачем строятся планы скоростей?» - студенты вразумительно ответить не могут. Как правило, приходится слышать что-то вроде: «- Для определения величин и направлений скоростей точек». Это понятно. А для чего нужны величины и направления скоростей? Для удовлетворения любопытства? Обычно ответа нет. Отсюда следует, что роль планов скоростей и их значение для задач динамического синтеза и анализа понимается поверхностно.
Конечно, дело здесь не в любопытстве и не в стремлении нагрузить студента дополнительной малополезной работой. В задачах динамики механизмов кинематической характеристике «скорость» отводится особая роль. При помощи скоростей находят мощности сил сопротивлений и мощности движущих сил, осуществляют приведение сил, выполняют силовые расчеты, энергетические расчеты, расчеты КПД, строят планы ускорений и др. Другими словами, скорости нужны не сами по себе. Они используются, как промежуточный этап и необходимый инструмент решения более сложных задач ТММ.
Зная это, вопрос определения скоростей следует изучать основательно. Рассмотрим алгоритм построения планов скоростей, начиная с постановки задачи.[21]
Постановка задачи:
Дано:
1. План положения механизма (кинематическая схема механизма в заданном положении).
2. Скорость (угловая скорость) входного звена.
Определить:
1. Скорости характерных точек механизма (концевые точки звеньев и точки соединения звеньев).[22]
2. Скорости любых других точек механизма.
3. Угловые скорости звеньев.
Решение.
Порядок решения задачи проиллюстрируем на примере 2-х простых и одного более сложного механизмов (см. Примеры 1-3):
· Пример 1 - кривошипно-коромысловый механизм;
· Пример 2 - кривошипно-ползунный механизм;
· Пример 3 - кривошипно-ползунный механизм с промежуточной кулисой.
Построение планов скоростей для сложных механизмов является компиляцией операций, которые выполняются для этих простых.
Пример 1.
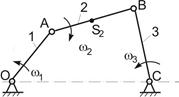
| 
|
| Рис. 4.3 | Рис. 4.4 |
Дано:
кривошипно-коромысловый механизм (Рис.4.3) в заданном положении;
звено 1 – входное; w1 – угловая скорость звена 1; AS2 = 0,5 · AB.
Определить:
скорости точек А, В, S2 графическим путем (построением плана скоростей).
Решение
Определение скоростей, как и любая другая задача кинематического анализа, выполняется поэтапно, в последовательности, предопределенной формулой строения механизма.
В нашем случае формула строения имеет вид: I (0,1) → II (2,3).
Из формулы следует порядок возможных действий:
- определение и изображение на чертеже скоростей точек первичного механизма;
- определение и изображение скоростей точек и угловых скоростей звеньев структурной группы II (2,3).
Следуя этому порядку, первоначально изображают на чертеже скорости характерных точек механизма (концевых точек звеньев и точек подвижных соединений звеньев). Полученный «базовый» план скоростей используют для определения абсолютных значений скоростей самих характерных точек механизма и угловых скоростей звеньев. На втором этапе построений находят и изображают на плане скорости любых других точек.
Реализуем данный алгоритм для построения плана и определения скоростей точек и звеньев нашего механизма.
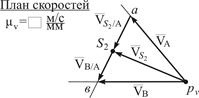
1. Определим и изобразим на плане (Рис.4.4) скорость точки А.
Точка А является характерной точкой механизма. Она принадлежит звену 1, которое вращается вокруг неподвижного центра О с угловой скоростью  .
.
Поэтому:
- величина скорости т. А: 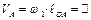 (4.1)
(4.1)
- направление скорости т. А: 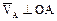 в направлении
в направлении  .
.
Для графических построений выберем масштабный коэффициент плана скоростей:
 (4.2)
(4.2)
Из (4.2) следует, что скорость  на плане будет изображена отрезком длиной
на плане будет изображена отрезком длиной  . В поле чертежа выберем произвольную точку
. В поле чертежа выберем произвольную точку 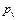 - полюс плана скоростей. Изобразим вектор
- полюс плана скоростей. Изобразим вектор  =
= , отложив его от точки
, отложив его от точки 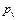 перпендикулярно ОА в направлении угловой скорости кривошипа.
перпендикулярно ОА в направлении угловой скорости кривошипа.
2. Определим и изобразим на чертеже скорость точки В.
Точка В также является характерной точкой механизма. Это общая точка для звеньев 2 и 3. Для определения скорости точки В следует графически решить систему векторных уравнений:
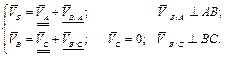 (4.3)
(4.3)
В системе (4.3) двумя чертами подчеркнуты векторы, величина и направление которых в данный момент являются известными. Одной чертой подчеркнуты векторы, у которых известно только их направление. Если известные векторы  и
и  отложить из одной точки (например, из полюса
отложить из одной точки (например, из полюса 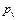 ) и дорисовать к ним направления
) и дорисовать к ним направления 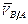 и
и  , то задачу по определению неизвестного вектора
, то задачу по определению неизвестного вектора 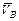 можно решить графически. Тогда точка
можно решить графически. Тогда точка 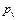 будет началом, а точка «в» (полученная на пересечении направлений
будет началом, а точка «в» (полученная на пересечении направлений 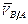 и
и  ) - концом вектора
) - концом вектора 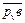 =
=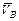 , удовлетворяющего одновременно обоим уравнениям системы.
, удовлетворяющего одновременно обоим уравнениям системы.
Таким образом, величины и направления 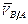 и
и  - также становятся определенными. С учетом
- также становятся определенными. С учетом  , имеем
, имеем  =
= . Численное значение величины
. Численное значение величины  найдем из плана, измерив длину отрезка
найдем из плана, измерив длину отрезка  :
:
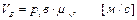
Базовый план скоростей построен.
Переходим к определению скоростей других точек. Такой точкой по условию задачи является точка 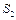 - центр масс звена 2.
- центр масс звена 2.
3. Определим скорость точки 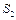 .
.
Скорость т.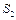 находим по аналогичной векторной формуле. В этом случае система уравнений не понадобится, т.к. вектор
находим по аналогичной векторной формуле. В этом случае система уравнений не понадобится, т.к. вектор  определен ранее, а величина и направление
определен ранее, а величина и направление  легко определяется (на основании известного
легко определяется (на основании известного 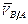 ).
).
 (4.4)
(4.4)
4. Определим угловые скорости звеньев 2 и 3:
Угловые скорости  и
и 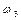 найдем по формулам:
найдем по формулам:
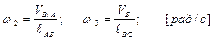 (4.5)
(4.5)
Направления  и
и 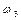 изображаем на рис.4.3 в соответствии с направлениями
изображаем на рис.4.3 в соответствии с направлениями  и
и  на плане скоростей.
на плане скоростей.
Пример 2.

| 
|
| Рис.4.5 | Рис. 4.6 |
Дано:
кривошипно-ползунный механизм (Рис.4.5) в заданном положении;
звено 1 – входное; w1 - угловая скорость звена 1; AS2 = 0,5 · AB.
Определить:
скорости точек А, В, S2 путем построения плана скоростей.
Решение
Последовательность и логика построений в данной задаче и в Примере 1 являются аналогичными. Поэтому, решение приводим в конспективном виде.
1) 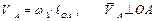 ;
;
2) 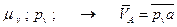 ;
;
3) 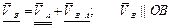 ;
; 

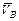 ;
; 
4)  ;
; 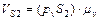 ;
;
5) 
Пример 3.
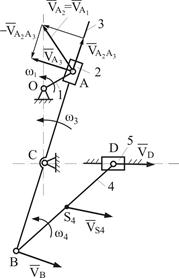
| 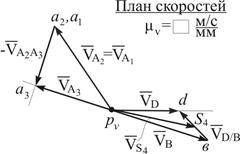
|
| Рис. 4.7 | Рис. 4.8 |
Дано:
кривошипно-ползунный механизм с промежуточной кулисой (Рис.4.7) в заданном положении; звено 1 – входное; w1 - угловая скорость звена 1;
ВS4 = 0,5 · BD.
Определить:
скорости точек A, B, D, S4 путем построения плана скоростей.
Решение.
Ряд пунктов приведенного ниже алгоритма выполняются аналогично предыдущим примерам и не требуют пояснений. Затруднения могут возникнуть при определении скоростей точек структурной группы (2,3), звенья которой образуют между собой поступательную пару. Построение плана скоростей в этом случае имеет свои особенности, на которые следует обратить внимание (см. пп.2-3 алгоритма).
При построении планов скоростей кулисных механизмов характерным является использование уравнений, связывающих скорости двух точек, совпадающих в данном положении, но принадлежащих разным звеньям поступательной пары. В нашем примере таким точками будут точки 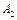 и
и  (Рис.4.7). Точки
(Рис.4.7). Точки 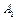 и
и 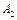 совпадают с центром вращательной пары, соединяющей звенья 1 и 2. Поэтому
совпадают с центром вращательной пары, соединяющей звенья 1 и 2. Поэтому  . Точка
. Точка  в данный момент совпадает по положению с точками
в данный момент совпадает по положению с точками 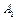 и
и 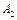 , но принадлежит звену 3.
, но принадлежит звену 3.
Рассматривая движение звена 2 как сложное, представим его в виде суммы двух движений: переносного вращательного со звеном 3 и относительного поступательного вдоль звена 3.
Тогда, для точки 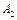 звена 2 получим векторное уравнение:
звена 2 получим векторное уравнение:
 , (4.6)
, (4.6)
где  - абсолютная скорость т.
- абсолютная скорость т.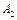 ;
;
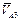 - переносная скорость т.
- переносная скорость т.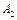 , в данный момент совпадающая со скоростью т.
, в данный момент совпадающая со скоростью т. звена 3;
звена 3;
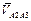 - скорость т.
- скорость т.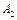 при относительном движении звена 2 по звену 3.
при относительном движении звена 2 по звену 3.
Из (4.6) можно получить уравнение с неизвестным вектором в левой части:
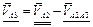 (4.7)
(4.7)
Для графического решения уравнения (4.7) из полюса 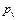 в масштабе
в масштабе 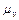 откладываем известный вектор
откладываем известный вектор  (Рис.4.8). Через точку
(Рис.4.8). Через точку 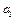 (или совпадающую с ней точку
(или совпадающую с ней точку  ) конца векторов
) конца векторов  проводим прямую, направленную параллельно
проводим прямую, направленную параллельно  . На этой прямой будет находиться вектор
. На этой прямой будет находиться вектор  . Одновременно, через полюс
. Одновременно, через полюс  проводим прямую, перпендикулярную
проводим прямую, перпендикулярную  . На ней будет лежать вектор
. На ней будет лежать вектор 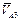 . Пересечение этих прямых даст точку
. Пересечение этих прямых даст точку  , определяющую величины векторов
, определяющую величины векторов 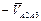 и
и 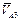 .
.
Если скорость 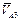 т.
т. известна, то легко определить скорость т.
известна, то легко определить скорость т.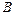 , также принадлежащей звену 3, которое вращается вокруг т.
, также принадлежащей звену 3, которое вращается вокруг т.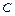 (см. п.4 алгоритма).
(см. п.4 алгоритма).
Построение плана скоростей для данной задачи можно представить в виде алгоритма действий, приведенного ниже.
1) 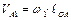 ;
;  ;
;  (Рис.4.8);
(Рис.4.8);
2)  ;
; 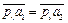 ;
;
3)  ;
; 
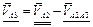
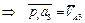 ;
;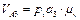 ;
;
4)  ;
;
5)  ;
; 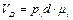 ;
;
6)  ,
,  ;
;
7) 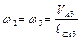 ;
; 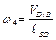 ;
; 
 ;
;  ;
;  .
.
4.4. Определение ускорений точек (построение планов ускорений) и угловых ускорений звеньев механизма
Как и планы скоростей, планы ускорений, как правило, строят не ради самих ускорений, а с целью дальнейшего их использования.
Одно из возможных направлений этого использования - силовой анализ механизма. Если силовой расчет выполняется по методу кинетостатики, ускорения необходимы для определения фиктивных сил инерции (сил инерции Даламбера). Таким образом, определение ускорений (как и определение скоростей) - не самоцель. Обычно, это промежуточный этап решения более сложной задачи.
Рассмотрим построение планов ускорений на примерах 2-х простых механизмов.
Постановка задачи
Дано:
- План механизма в заданном положении.
- Угловая скорость и угловое ускорение ведущего звена.
- Угловые скорости всех других звеньев механизма.
Определить:
- Ускорения характерных точек (точки соединения звеньев).
- Ускорения других точек.
- Угловые ускорения звеньев.
Пример 1. – кривошипно-коромысловый механизм (Рис.4.9)

| 
|
| Рис. 4.9 | Рис. 4.10 |
Решение
1. Определим ускорение точки А
 (4.8)
(4.8)
 (4.9)
(4.9)
Направления:  (Рис.4.10)
(Рис.4.10)
2. Выберем масштабный коэффициент плана ускорений и построим вектор 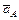 :
:
 (4.10)
(4.10)
 ;
;  ;
; 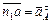 ;
; 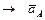
3. Определим ускорение точки 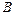 (точка
(точка 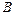 принадлежит 2-м звеньям)
принадлежит 2-м звеньям)
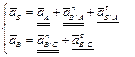

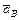 (4.11)
(4.11)
 ;
; 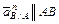 ;
; 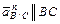 (4.12)
(4.12)
4. Определим значения абсолютных и относительных ускорений точек
 и т.д. (4.13)
и т.д. (4.13)
5. Определим угловые ускорения звеньев
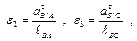 (4.14)
(4.14)
Направления и
и показываем соответственно направлениям
показываем соответственно направлениям  и
и  .
.
Пример 2. – кривошипно-ползунный механизм (Рис.4.11)

| 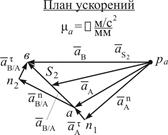
|
| Рис. 4.11 | Рис. 4.12 |
Алгоритм построений (Рис.4.12)
1.  ;
;
2.  ;
; 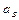 = …;
= …;
3. 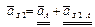 ;
; 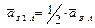 ;
;
4. 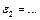 ,
,  .
.
4.5. Кинематический анализ сложных механизмов
Кинематический анализ сложных механизмов выполняется в последовательности, определяемой формулой строения механизма, т.е.:
1. Анализ механизма I класса.
2. Анализ группы Ассура, следующей за механизмом I класса.
3. Анализ последующих групп Ассура.
В качестве примера рассмотрим механизм, изображенный на рис.4.13.
Формула строения этого механизма: I(0,1)® II(2,3) ® II(4,5)
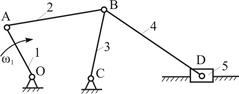 Рис. 4.13
Рис. 4.13
| Решение.
1. Определение кинематических характеристик звена 1: положение, угловая скорость, угловое ускорение (если не заданы) и кинематических характеристик точки А 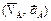 . .
|
2. Определение кинематических характеристик точек и звеньев группы Ассура II(2,3) – положение, 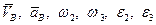 .
.
3. Определение кинематических характеристик точек и звеньев группы Ассура II(4,5) – положение, 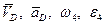 .
.
Таким образом, задача по определению кинематических характеристик для механизма (рис.4.13) сводится к последовательному решению задач для кривошипно-коромыслового, а затем коромыслово-ползунного механизмов (которые рассмотрены ранее в примерах).
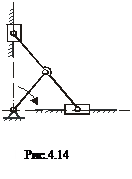 Задание для самостоятельной работы и самоконтроля усвоения материала:
Задание для самостоятельной работы и самоконтроля усвоения материала:
Дано: На рис.4.14 показана кинематическая схема эллипсографа - прибора для построения правильных эллипсов. Геометрические размеры таковы, что  .
.
Требуется: Доказать, что точки, принадлежащие шатуну эллипсографа двигаются по эллиптическим траекториям. Задачу решить графическим методом. Результаты сравнить с данными аналитического решения.
Аналитическое решение
1. W = 3 n - 2 p5 - p4 = 3 × 3 – 2 × 4 = 1

(1 зв. + 2 к/пары – “лишние”, т.к. не влияют на
движение механизма)
2. Определим координаты произвольной точки М (Рис.4.15), а затем, исключив параметр  , найдем уравнение траектории движения этой точки:
, найдем уравнение траектории движения этой точки:

(r + BM) = A1 = const
(r - BM) = A2 = const
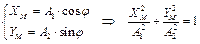 (4.15)
(4.15)
Уравнение (4.15) – уравнение эллипса.
Замечание. В лекции не рассмотрено построение плана ускорений для кулисного механизма. Желающим разобраться в этом вопросе рекомендуем обратиться к учебнику [3], Глава 2, §4.
Вопросы для самоконтроля
1. Назовите задачу и цели кинематического исследования механизмов.
2. Каким основным признаком руководствуются при построении крайних положений четырехзвенных кривошипно-коромыслового или кривошипно-ползунного механизмов?
3. Какое положение занимает кривошип по отношению к кулисе в крайних положениях кривошипно-кулисного механизма?
4. Объясните общий порядок построения планов скоростей и ускорений для рычажных механизмов II класса.
5. Масштабные коэффициенты планов скоростей и ускорений. Какова их размерность? Как вычисляются значения масштабных коэффициентов?
6. Нарисуйте звено АВ длиной  . Покажите на рисунке заданные параметры
. Покажите на рисунке заданные параметры  ., указав их направления произвольно. Напишите векторные формулы для определения скорости и ускорения точки В. Определите
., указав их направления произвольно. Напишите векторные формулы для определения скорости и ускорения точки В. Определите 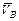 и
и 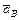 . путем схематических графических построений.
. путем схематических графических построений.
7. Изучив разделы 4.3 и 4.4 лекции 4, постройте схематический план скоростей (показать только направления векторов) и схематический план ускорений для механизма, изображенного на рис.4.13.
Лекция 5
кинематический анализ плоских рычажных механизмов (аналитический метод)
5.1. Определение положений механизма. ([1], §23, 24, 25; [2], §3.3)
5.2. Определение скоростей точек и угловых скоростей звеньев механизма. ([1], §23, 24, 25; [2], §3.3)
5.3. Определение ускорений точек и угловых ускорений звеньев механизма. ([1], §23, 24, 25; [2], §3.3)
5.4. Кинематический анализ сложных механизмов. ([1], §26; [2], §3.3)
Кинематический анализ механизмов аналитическим методом выполняется с помощью ПК или другой вычислительной техники. Для этого составляется соответствующая программа вычислений, в которую входят формулы для определения положений звеньев и их кинематических характеристик. Если механизм имеет степень подвижности, равную 1, то все кинематические параметры должны определяться исходя из одной величины – обобщенной координаты (для механизмов с ведущим кривошипом, исходя из положения кривошипа).
В основу аналитического решения задачи положен метод замкнутых векторных контуров, предложенный В.А.Зиновьевым.[23]
Покажем получение основных формул кинематического анализа на примере шарнирного четырехзвенника (Рис.5.1).
5.1. Определение положений механизма.
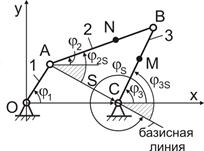 Дано:
Дано:
ОА, АВ, ВС, ОС (Рис.5.1);
j 1 – положение начального звена 1;
w1 – угловая скорость звена 1;
e1 –угловое ускорение звена 1.
Определить:
j2(j1), j3(j1) -?
Рис. 5.1.
Решение
1) Выберем систему координат хоу с началом в точке О (Рис.5.1).
Рассмотрим векторный контур ОАС, в котором
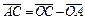 (5.1)
(5.1)
Принимая  , попытаемся определить зависимости
, попытаемся определить зависимости  и
и 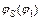 .
.
Для этого спроецируем (5.1) на оси х и у:
пр. х g  (5.2)
(5.2)
пр. y g 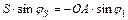 (5.3)
(5.3)
При этом 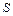 и
и  - неизвестные параметры.
- неизвестные параметры.
Выполним преобразования, разделив (5.3) на (5.2):
(5.3): (5.2) g  , (5.4)
, (5.4)
т.е. получили зависимость  .
.
Продолжим преобразования с выражениями (5.3) и (5.2):
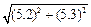 g
g 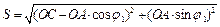 (5.5)
(5.5)
т.е. получили зависимость  .
.
2) Рассмотрим векторный контур  и определим
и определим 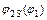 и
и  .
.
 , (5.6)
, (5.6) 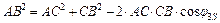 , (5.7)
, (5.7)
В (5.6) и (5.7) известно все, кроме j2S и j3S, которые легко определить.
 , (5.8)
, (5.8)
т.е. получена зависимость 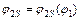 .
.
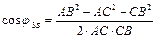 , (5.9)
, (5.9)
т.е. получена зависимость  .
.
3) Определим  и
и  .
.
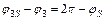 ; (5.10)
; (5.10)
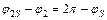 ; (5.11)
; (5.11)
Отсюда:  ,т.е. имеем
,т.е. имеем ; (5.12)
; (5.12)
 , т.е.
, т.е. (5.13)
(5.13)
Таким образом, в результате выполнения пп. 1÷3 определено  и
и  , т.е. положение звеньев, как функция, положения ведущего звена.
, т.е. положение звеньев, как функция, положения ведущего звена.
4) При необходимости можно определить положение точек, принадлежащих звеньям 2 или 3 (например, координаты 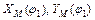 и,
и,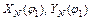 - см. рис.5.1). Покажем эту возможность.
- см. рис.5.1). Покажем эту возможность.
Найдем проекции положения точек М и N на оси х и у:
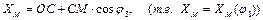 (5.14)
(5.14)
 (5.15)
(5.15)
 (5.16)
(5.16)
 (5.17)
(5.17)
Поскольку 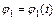 , то полученные выше формулы позволяют найти
, то полученные выше формулы позволяют найти 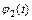 ,
,  ,
, 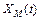 ,
,  ,
, 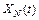 ,
, 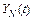 .
.
Задача определения положений звеньев и точек звеньев в функции от угла поворота  выполнена.
выполнена.
5.2. Определение скоростей точек и угловых скоростей звеньев механизма.
Скорости точек и угловые скорости звеньев можно найти через соответствующие аналоги скоростей:
 , (5.18)
, (5.18)
где  - аналог угловой скорости звена 2; (5.19)
- аналог угловой скорости звена 2; (5.19)
 , (5.20)
, (5.20)
где  - аналог угловой скорости звена 3; (5.21)
- аналог угловой скорости звена 3; (5.21)
При этом 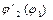 и
и 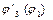 не зависят от w1.
не зависят от w1.
Таким образом, чтобы найти 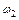 и
и 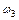 , достаточно найти аналоги
, достаточно найти аналоги 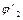 и
и  .
.
Определим аналоги угловых скоростей, используя метод замкнутых векторных контуров:
Контур ОАВС (Рис.5.1)
 (5.22)
(5.22)
Спроецируем (5.22) на оси х и у:
пр. х ® 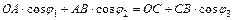 (5.23)
(5.23)
пр. у ®  (5.24)
(5.24)
Возьмем производную по  , учитывая, что
, учитывая, что  и
и 
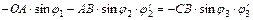 (5.25)
(5.25)
 (5.26)
(5.26)
Если выполнить ® (5.25) ´ cos j3 + (5.26) ´ sin j3 , получим:
 (5.27)
(5.27)
Отсюда:
 , т.е.
, т.е.  (5.28)
(5.28)
Если выполнить ® (5.25) ´ cos j2 + (5.26) ´ sin j2 , аналогично получим:
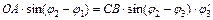 (5.29)
(5.29)
Откуда:
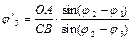 , т.е.
, т.е.  (5.30)
(5.30)
Если известны аналоги (5.28) и (5.30), легко определить w2 и w3 из (5.18) и (5.20).
Определим скорости точек
Начнем с простого – точка В и точка М.
 ; (5.31)
; (5.31)
 ; (5.32)
; (5.32)
 (5.33)
(5.33)
Скорость точки N вычислим по проекциям:
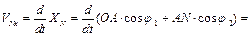

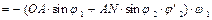 ; (5.34)
; (5.34)

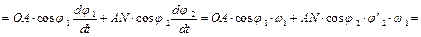


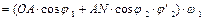 (5.35)
(5.35)
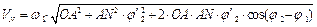 (5.36)
(5.36)
По аналогии с введенными ранее понятиями аналогов угловых скоростей можно ввести понятия аналогов скоростей точек А, В, М, N.
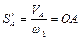 ; (5.37)
; (5.37)
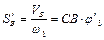 ; (5.38)
; (5.38)
 ; (5.39)
; (5.39)
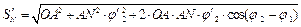 (5.40)
(5.40)
5.3. Определение ускорений точек и угловых ускорений звеньев механизма.
Для определения ускорений используют аналоги ускорений:
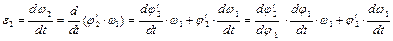 ;
;
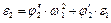 , (5.41)
, (5.41)
где  - аналог углового ускорения звена 2. (5.42)
- аналог углового ускорения звена 2. (5.42)
Аналогично:
 , (5.43)
, (5.43)
где  - аналог углового ускорения звена 3.
- аналог углового ускорения звена 3.
Таким образом, для определения e2 и e3 необходимо найти аналоги 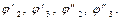
Определим аналоги угловых ускорений (Рис. 5.1).
Продифференцируем уравнения (5.25) и (5.26) по j1, учитывая, что j2(j1), j3(j1),  .
.

=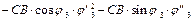 ; (5.44)
; (5.44)
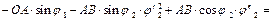
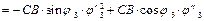 ; (5.45)
; (5.45)
Если выполнить ®