
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Порядок проведения структурного анализа
|
|
|
|
ПРИНЦИП ОБРАЗОВАНИЯ МЕХАНИЗМОВ ПО Л.В. АССУРУ. КЛАССИФИКАЦИЯ СТРУКТУРНЫХ ГРУПП ПО Л.В. АССУРУ
И ПЛОСКИХ МЕХАНИЗМОВ
Кинематическая цепь и, следовательно, механизм, обладает определенным числом степеней свободы и степенью подвижности, зависящими от числа звеньев и кинематических пар.
Как указывалось в параграфе § 1.2, если на движение звена в пространстве не наложено никаких условий связи, то оно обладает шестью степенями свободы (подвижности). Если число звеньев кинематической цепи равно n, то общее число подвижности W, которыми обладают n звеньев до их соединения в кинематические пары, равно 6n.
W = 6n. (1.1)
Число пар I класса равно p1, II класса равно p2, III класса - p3, IV класса - p4, V класса - p5. После соединения кинематических пар в кинематические цепи исключается одна связь каждого класса. Поэтому число степеней подвижности пространственной кинематической цепи будет равна:
W=6n-(6-1)p5-(6-2)p4-(6-3)p3-(6-4)p2-(6-5)p1.
После преобразования имеем:
W = 6n - 5p5 - 4p4 - 3p3 - 2p2 - p1. (1.2)
Формула (1.2) - формула для определения степени подвижности пространственных механизмов. Была выведена русскими учеными: П.И. Сомовым в 1887 г., А.П. Малышевым в 1923 г.
Плоские кинематические цепи образованы кинематическими парами только V и IV классов. Поэтому формула (1.2) примет вид:
W = 6n - 5p5 - 4p4.
После преобразования имеем:
W = 3n - 2p5 - p4. (1.3)
Формула (1.3) - формула для определения степени подвижности плоских механизмов. Была выведена русским ученым П.Л. Чебышевым в 1870 г. Здесь:
Ø n - число подвижных звеньев;
Ø p5 - число низших кинематических пар;
Ø p4 - число высших кинематических пар.
Клиновые механизмы состоят из поступательных кинематических пар V класса. Степень подвижности таких механизмов рассчитывается по формуле В.В.Добровольского
W = 2n - p5.(1.4)
В зависимости от числа W, стоящего в левой части уравнения, можно получать плоские механизмы, с одной, двумя, тремя и т. д. степенями свободы. Поэтому число степеней подвижности указывает на количество ведущих звеньев (кривошипов, двигателей).
При нулевой степени подвижности ни одно из звеньев кинематической цепи не может двигаться, и кинематическая цепь превращается в ферму. Для того, чтобы механизм двигался, нужно задаться движением хотя бы одного звена.
Принцип образования механизмов впервые был сформулирован в 1914 г. русским ученым Л.В. Ассуром. Он заключается в присоединении к ведущему звену групп звеньев, обладающих нулевой степенью подвижности.
Рассмотрим на примере.
К ведущему звену (кривошипу 1) присоединим кинематическую цепь, состоящую из звеньев 2 и 3. Получим четырехзвенный механизм, обладающий одной степенью подвижности (рисунок 1.7). Далее к третьему звену присоединим звенья 4 и 5. Получим шестизвенный механизм, также обладающий одной степенью подвижности (рисунок 1.8). Известно, что степень подвижности W указывает на число ведущих звеньев (§ 1.5). Так как после присоединения групп звеньев число W осталось неизменным, то кинематические цепи (2,3 и 4,5) обладают нулевой степенью подвижности по отношениям к звеньям 1 и 6.

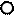
 А 2 В А 2 В
А 2 В А 2 В
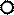



 1
1
 + 3 = 1 n1 3
+ 3 = 1 n1 3





 О
О
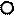 n1 О С
n1 О С





















 С
С
4 4 4
Рисунок 1.7 - Образование четырехзвенного механизма
W = 3n - 2p5 = 1(n = 3, p5 = 4)


 А 2 В B A B
А 2 В B A B

 n1
n1


 1 4 n1
1 4 n1





 О + + = D
О + + = D

































 С D O C
С D O C
6 5
5
6 6 6
Рисунок 1.8 - Образование шестизвенного механизма
W = 3n - 2p5 = 1 (n = 5, p5 = 7)
Кинематическая цепь, обладающая нулевой степенью подвижности по отношению к присоединяемым звеньям и не распадающаяся на более простые кинематические цепи, называется структурной группой или группой Ассура.
| |||
 | |||
1 n1


 О
О
 |
Рисунок 1.9 - WIкл = 3n - 2p5 - p4 = 1
(n=1, p5=1, p4=0)
Плоские кинематические цепи состоят из кинематических пар V класса. Поэтому степень подвижности структурных групп удовлетворяет условию:
W = 3n - 2p5 = 0
или
p5 =  . (1.5)
. (1.5)
Следовательно, число подвижных звеньев n, входящих в структурную группу, должно быть четным, а количество кинематических пар p5 целым числом.
Согласно формуле (1.5) структурные группы классифицируют по классам, исходя из количества подвижных звеньев и кинематических пар (таблица 1.2).
Структурная группа, имеющая два подвижных звена и три низшие кинематические пары, называется структурной группой II класса.
Таблица 1.2 - Классы структурных групп
| Параметр | II класс | III класс | IV класс | V класс | … |
| n | … | ||||
| p5 | … |
Механизмы, в состав которых входят структурные группы не выше 2 класса, называются механизмами II класса. Следовательно: класс механизма определяется по наивысшему классу структурной группы.
 На рассмотренном примере видно, что совокупность звеньев 2-3-4-5 хотя и обладает нулевой степенью подвижности, но не является группой Ассура, т.к. распадается на 2 кинематические цепи (звенья 2-3 и 4-5), каждая из которых также обладает нулевой степенью подвижности. Следовательно, данный механизм образован присоединением к механизму I класса двух групп Ассура. Количество структурных групп не влияет на число степеней подвижности. Действительно:
На рассмотренном примере видно, что совокупность звеньев 2-3-4-5 хотя и обладает нулевой степенью подвижности, но не является группой Ассура, т.к. распадается на 2 кинематические цепи (звенья 2-3 и 4-5), каждая из которых также обладает нулевой степенью подвижности. Следовательно, данный механизм образован присоединением к механизму I класса двух групп Ассура. Количество структурных групп не влияет на число степеней подвижности. Действительно:
W = W1кл + Wгр1 + Wгр2 = 1 + 0 + 0 = 1
Механизмы могут быть образованы также и присоединением групп Ассура одновременно к нескольким механизмам 1 класса. В этих случаях степень подвижности получаемых механизмов будет равна числу механизмов I класса (см. § 1.5).
Структурные группы II класса делятся на 5 видов
|
В


 2 3
2 3
А С
 |  |

 1 4
1 4
Рисунок 1.10, а
соединение звеньев либо с другой структурной группой, либо с опорой, либо с механизмом I класса.
Остальные виды получаются путем замены внешних или внутреннего шарниров, т.е. вращательных кинематических пар на поступательные.
 | |||
| |||

 | ||||||
 |  | |||||
 | ||||||
 | ||||||
Структурная формула структурной группы записывается в квадратных скобках дробью. В числителе записываются номера звеньев, входящих в структурную группу. В знаменателе записываются наименование кинематических пар, начиная с внешнего шарнира. Перед скобками ставится класс группы Ассура, после скобок – вид структурной группы.
Пример выполнения структурной формулы
структурной группы II класса, 2 вида
 (1.6)
(1.6)
1. Пронумеровать звенья. Нумерация начинается с того звена, где задано вращение (n1, ω1). Неподвижные звенья (стойки, опоры) обозначаются одной (последней) цифрой.
2. Рассчитать степень подвижности механизма. По степени подвижности определить количество ведущих звеньев (кривошипов, механизмов I класса). Дать названия звеньям механизма.
3. Начиная с последней структурной группы, считая от ведущего звена, выделить группы Ассура II, III и т.д. классов, так, чтобы остался свободным механизм I класса (ведущее звено со стойкой).
4. Изобразить структурные группы в том же масштабе, что и механизм, начиная с последней. Для каждой структурной группы рассчитать степень подвижности и изобразить структурную формулу (см. формулу 1.6). Определить класс и вид структурной группы.
5. Изобразить механизм I класса. Рассчитать степень его подвижности, записать структурную формулу.
6. Составить структурную формулу всего механизма в порядке присоединения структурных групп к механизму I класса. Определить класс всего механизма. Класс всего механизма определяется по наивысшему классу структурной группы.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 569; Нарушение авторских прав?; Мы поможем в написании вашей работы!