Определение интеграла Римана

Пусть функция F(x) задана в некотором промежутке [a,b]. Разобьём этот промежуток произвольным образом на части.

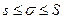
Наибольшую из разностей 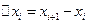, i=0,1,2,3,…,n-1

Обозначим :

Возьмём в каждом из частичных промежутков 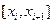произвольную точку , , i=0,1,2,3,…,n-1 и составим сумму: 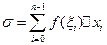(1)

Эта сумма называется интегральной суммой.

Определение. Говорят, чтосумма 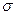при 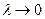имеет конечный предел I, если для каждого числа 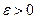найдётся такое 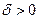, что, как только , так сейчас же 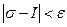при любом выборе чисел .

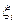Записывается это так: , (2)

Конечный предел 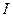суммы 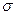при 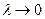называется определённым интегралом функции f(x) в промежутке от a до b и обозначается символом:

, (3)

В случае существования такого предела функция f(x) называется интегрируемой в [a,b];

Числа a и b называются соответственно нижним и верхним пределами интеграла. При постоянных пределах a и b определённый интеграл представляет собой постоянное число.

Приведённое определение интеграла принадлежит Риману. Сумму 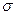иногда называют Римановой суммой.

Замечание. Высказанное определение в действительности может быть приложено лишь к ограниченной функции. В самом деле, если бы функция f(x) была в [a,b] неограниченна, то – при любом разбиении промежутка на части она сохранила бы подобное свойство хоть в одной из частей. Тогда за счёт выбора в этой части точки можно было бы сделать , а с ней и сумму 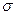, сколько угодно большой; при этих условиях конечного предела для 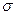существовать не могло бы.

Итак, интегрируемая функция необходимо ограничена.

Далее мы будем наперёд предполагать рассматриваемую функцию f(x) ограниченной, то есть .

Рассматривая график функции f(x) на [a,b] легко усмотреть геометрический смысл интегральной суммы, а вместе с ней и определённого интеграла. В самом деле, как это видно из рис.1,интегральная сумма представляет собой сумму площадей прямоугольников, образующих ступенчатую фигуру, контур которой заштрихован на рис.1.

рис.1.

Из геометрического смысла интегральной суммы непосредственно следует, что в том случае, когда 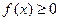, величину определённого интеграла 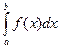естественно принять за число, измеряющее площадь фигуры, ограниченной графиком функции f(x), прямыми и , и отрезком оси x между точками a и b. Эту фигуру называют криволинейной трапецией.

Дата добавления: 2014-01-20