III.Условие существования интеграла

Теорема. Для существования определённого интеграла необходимо и достаточно, чтобы было

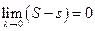, (5)

Доказательство:

Необходимость:

Дано: определённый интеграл существует.

Требуется доказать:

.

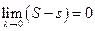Определённый интеграл существует, следовательно, существует предел:

,

Следовательно, по любому 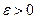можно указать 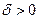такое, что, как только все 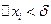, так сейчас же 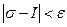. При любом выборе точек 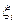в пределах соответствующих промежутков. Последнее неравенство означает, что

,

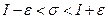т.е. числа 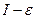и 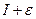являются нижней и верхней границами множества интегральных сумм, отвечающих всем достаточно мелким разбиением.

Для этих же разбиений, суммы Дарбу являются точными границами, следовательно, .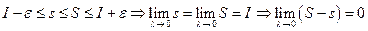

Ч.т.д.

Достаточность:

Дано: .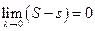

Требуется доказать, что определённый интеграл существует т.е. 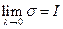. Из условия 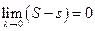и условия 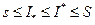, следует, что 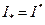. Обозначим общее значение 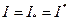. Тогда 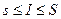. С другой стороны, если 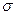одно из значений интегральной суммы, отвечающей тому же разбиению промежутка, что и суммы 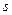и 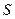, то, как мы знаем, .

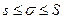Согласно (5), если предположить 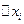достаточно малым, суммы 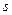и 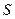разнятся меньше, чем на произвольное 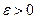. Но в таком случае это справедливо и относительно заключённых между ними чисел 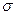и 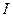, т.е.

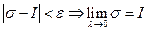
Теорема доказана.

Замечание. Если обозначить колебание 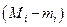функции в i-ом частичном промежутке через 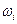, т.е. 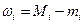, то будем иметь

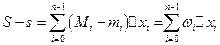
И условие существования определённого интеграла может быть переписано так:

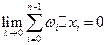, (6)

Теорема Кантора. Если функция определена и непрерывна в замкнутом промежутке , то она и равномерно непрерывна в этом промежутке.

Следствие (из теоремы Кантора).

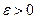Пусть функция определена и непрерывна в замкнутом промежутке . Тогда по замкнутому найдётся такое 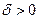, что если промежуток произвольно разбить на части с длинами, меньшими 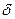, то в каждом из них колебание функции будет меньше .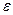

Классы интегрируемых функций.

I.Если функция непрерывна в , то она интегрируема.

Доказательство:

Раз непрерывна, то основании следствия из теоремы Кантора по заданному 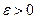всегда найдётся 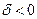, что лишь только промежуток разбит на части с длинами 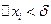, то все 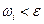. Отсюда:

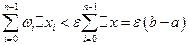
Так как 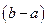- постоянное число, а 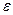произвольно мало, то условие (6) выполняется, а из него вытекает существование интеграла.

II.Если ограниченная функция в имеет лишь конечное число точек разрыва, то она интегрируема.

Доказательство:

Пусть точки разрыва будут 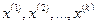. Возьмём произвольно 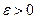. Окружим точки разрыва окрестностями.

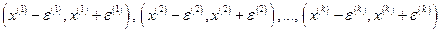
Таким образом, чтобы длина каждой была меньше 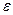. В оставшихся, замкнутых, промежутках функция будет непрерывной, и мы можем применить к каждому из них в отдельности следствие из теоремы Кантора. Из полученных по 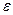чисел 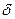выберем наименьшее (его тоже обозначим 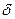). Тогда оно будем годиться для любого из указанных промежутков. Ничто нам не мешает взять при этом 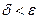. Разобьём теперь наш промежуток на части так, чтобы их длины 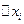все были меньше 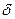. Полученные частичные промежутки будут двух родов:

1)Промежутки, лежащие целиком вне выделенных окрестностей около точек разрыва. В них колебание функции .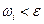

2)Промежутки, любо заключённые целиком внутри выделенных окрестностей, любо частью на эти окрестности налегающие.

Так как функция предположена ограниченной, то колебание её 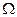во всём промежутке будет конечно; колебание же в любом частичном промежутке не превосходящий 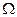. Сумму 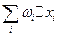разобьём на две:

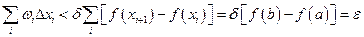
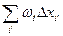и ,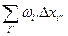

распространённые, соответственно на промежутке первого и второго рода.

Для первой суммы, как и в предыдущей теореме, будем иметь:

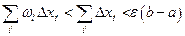
Что касается второй суммы, то заметим, что длины промежутков второго рода, целиком попавших внутрь выделенных окрестностей, в сумме 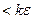; промежутков же, лишь частично налегающих на них, может быть не больше 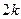, и сумма их длин 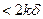, а значит и подавно 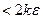. Следовательно,

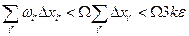
Таким образом, окончательно, при 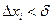имеем:

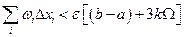
Это и доказывает наше утверждение, так как в квадратных скобках содержится постоянное число, а 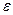произвольно мало.

III.Монотонная ограниченная функция всегда интегрируема.

Доказательство:

Пусть монотонно возрастающая функция. Тогда её колебание в будет 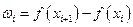. Зададим любое 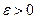и положим .

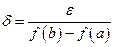Как только 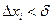, тотчас будем иметь:

,

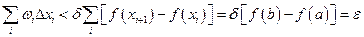откуда и следует интегрируемость функции.

Дата добавления: 2014-01-20