Методом моментов

Приближенное решение обыкновенных дифференциальных уравнений

Рассмотрим уравнение

(*)

где A, K – линейные операторы из банахова пространства E в гильбертово F, с плотными в E областями определения . Пусть A обратим, ограничен и определен на всем F, оператор 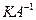вполне непрерывен в F и 1 не является его собственным значением. Тогда L обратим; 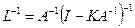ограничен и определен на всем F.

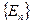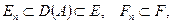
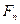Пусть и - две последовательности конечномерных подпространств, - ортопроектор F на . Приближенное решение ищется из условия

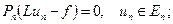(1)

Это метод Галеркина – Петрова.

Теорема 1. Пусть последовательност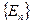и и связаны соотношением

, (2)

где S – вполне непрерывный оператор в F, для которого 1 не является собственным значением. Пусть последовательность подпространств предельно плотна в F. Тогда при достаточно больших n существует единственное удовлетворяющее условиям (1) приближение и справедлива оценка

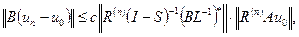(3)

где – точное решение уравнения, , - ортопроектор из F на , B - любой линейный оператор с областью определения 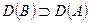в E и областью значений в некотором банаховом пространстве E’ и такой, что 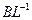– ограниченный оператор.

Приведем приложение теоремы 1 для краевых задач.

Рассмотрим снова линейное дифференциальное уравнение

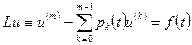(4)

при линейных однородных краевых условиях

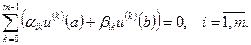(5)

Будем предполагать, что однородное уравнение имеет при краевых условиях (5) только тривиальное решение .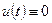

Метод моментов заключается в следующем. Приближенное решение краевой задачи (4) – (5) ищется в виде

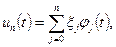(6)

где 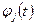- многочлен степени m + j, удовлетворяющий краевым условиям (5). Пусть кроме Lu задано еще второе дифференциальное выражение

.

Постоянные 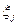определяются из условий

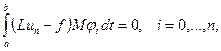(7)

равносильных системе линейных уравнений

(8)

Для практических вычислений интересны случаи и , j= 0,…, m -1. В первом случае метод моментов переходит в метод наименьших квадратов, а второй случай интересен тем, что упрощает составление системы (8), т.к. тогда можно считать, что [1].

Через будем обозначать множество i- 1 раз абсолютно непрерывно дифференцируемых на функций 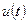таких, что . Норма 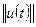ниже означает норму в .

Теорема 2. Пусть каждый коэффициент непрерывно дифференцируем j раз, 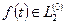и , j= 0,…, m -1, 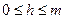. Пусть каждое из однородных уравнений Lu= 0 и Mu= 0 имеет при краевых условиях (5) лишь нулевое решение.

Тогда при достаточно больших n система уравнений (8) однозначно разрешима и справедливы оценки

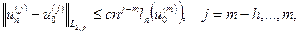(9)

(10)

где - точное решение краевой задачи (4) – (5), а

- наилучшее среднеквадратичное приближение функции 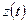многочленами степени .

При доказательстве используется следующая оценка среднеквадратичного приближения функций:

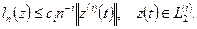(11)

[1] Более справедливо называть (6) – (8) методом обобщенных моментов, сохранив название «метод моментов» для случая , j= 0,…, m -1.

Дата добавления: 2014-01-20