Гибкого звена механизма

Преобразование движения по принципу деформирования

Сопоставляя структурную схему волновой передачи со структурными схемами ранее известных передач, можно отметить следующие принципиальные различия: 1) все ранее известные механические передачи являются механизмами с жесткими звеньями; волновая передача содержит гибкое звено; 2) во всех передачах с жесткими звеньями преобразование движения осуществляется по принципу рычага или по принципу наклонной плоскости; принцип рычага используется в известных зубчатых, фрикционных, ременных и цепных передачах; по принципу наклонной плоскости работают червячные и винтовые передачи.

Рис.11.3

В волновой передаче преобразование движения осуществляется за счет деформирования гибкого звена. Этот новый принцип будем называть принципом деформирования. Сущность принципа деформирования поясняется простейшим примером – рис.11.3. На этом рисунке гибкая

нерастяжимая лента нагружена силами Р₁ и Р₂. В положении равновесия лента получила перемещения W в направлении Р₁ и u против направления Р₂.

Из условий равновесия получаем

(Р₂ / Р₁) = (1/2 sin g) – своеобразное передаточное отношение по силам.

В этом своеобразном механизме поперечное перемещение w преобразуется в продольное u через деформирование ленты.

Величина передаточного отношения зависит от величины перемещения w или от угла g. При малых g можно получить очень большие передаточные отношения (при g ® ® ¥).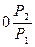

Рассмотренный механизм (см.рис.11.3) является механизмом разового или пульсирующего действия с переменным передаточным отношением. Это затрудняет его применение в технике. Однако преобразование движения по принципу деформирования здесь очевидно.

Изобретатели волновой передачи превратили этот механизм в механизм непрерывного действия с постоянным передаточным отношением. Для того чтобы понять преобразования движения в волновой передаче, рассмотрим движение точек невращающегося гибкого колеса при его деформировании вращающимся генератором. Отметим, что в нашей конструкции гибкое колесо подобно оболочке (толщина значительно меньше других размеров).

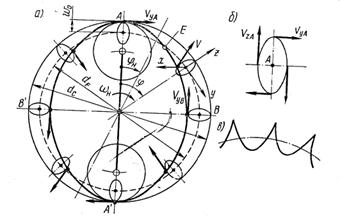
В теории оболочек обычно рассматривают перемещения точек срединной поверхности (поверхность посередине толщины оболочки) в координатах x, y, z (рис.11.4). Начало координат совмещают с положением рассматриваемой точки до деформирования. Компоненты перемещений обозначают: W - радиальные

(ось z), u – окружные (ось у), u – осевые (ось х).

Рис.11.4

Перемещение u не оказывает влияния на кинематику передачи. Поэтому будем рассматривать плоскую задачу, в которой учитываем только W и u на торце цилиндра. Кроме того, в первом приближении не учитываем влияние толщины оболочки. Полагаем, что генератор обеспечивает деформирование торца цилиндра по форме, для которой

W = F₁ (j₁) (11.2)

где j₁ – угловая координата точки на срединной поверхности до деформирования, отсчитываемая от большой оси овала деформирования.

По условиям конструкции функция F₁ (j₁) должна быть периодической (период p) с максимумами в точках А и А’ и с минимумами в точках В и В’. при этом независимо от формы деформирования у фрикционных передач

W_max = W₀ (11.3)

а величина Wmin изменяется в зависимости от формы. Кроме того, F1 (j1) должна удовлетворять условию нерастяжимости срединной поверхности оболочки (длина периметра срединной поверхности не изменяется). Из этого условия получают зависимость между u и W - рис.11.5.

Рис.11.5

Перемещение элемента ab срединной поверхности до ее деформирования можно разбить на два этапа:

1) в положение a₂b₂ за счет радиальных перемещений W и (W + dW),

2) в положение a₁b₁ за счет окружных перемещений u и (u + du).

Приращение длины элемента: на первом этапе

a₂b₂ – ab = (r +W) dj – rd j = Wd j,

на втором этапе приращение равно разности окружных перемещений конца элемента (u + du) – u = du.

По условию нерастяжимости сумма приращений длины равна нулю:

Wd j + du = 0,

или

du / dj = –W, или условие нера-

u = –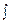W dj = F₂ (j₁) стяжимости (11.4)

Функции (11.2) и (11.4) выражают статическую форму гибкого колеса. При вращении генератора с угловой скоростью w_Н текущее положение рассматриваемой точки относительно его большой оси определяется углом j = j₁ - j_Н = j₁ – w_Нt. При этом формулы (11.2) и (11.4) можно записать в виде:

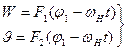(11.5)

Уравнения (11.5) определяют траекторию движения точки, расположенной под углом j₁. Здесь j₁ = const – начальный угол, а движение вызвано вращением генератора. Траектория выражается некоторой замкнутой кривой; на рис.11.4,а она изображена тонкой линией, на рис.11.4,б с увеличением. При вращающемся гибком колесе овальная траектория принимает форму, изображенную на рис.11.4,в.

За один оборот генератора любая точка невращающегося гибкого колеса совершает два пробега по своей траектории. Траектории всех точек гибкого колеса одинаковы. Движение по ним отличается только величиной фазы (фазовый угол j₁).

Дифференцируя функции (11.5) по времени, получаем компоненты скорости движения точек:

радиальная скорость

(11.6)

окружная скорость

.

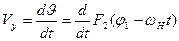Используя условие (), записываем

.

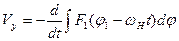В нашем случае j = j_Нt, при этом dj = -w_Нdt. Заменяя dj на -w_Нdt, получаем

(11.7)

Окружная скорость точки равна произведению ее радиального перемещения на угловую скорость генератора.

В соответствии с принятыми условиями для точек А и В, совпадающих с большой и малой осями овала, W_А = W₀ и W_В = – КW₀, где К – постоянная, зависящая от формы овала (для примера К = 1). При этом

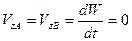(по условию максимума и (11.8)

минимума в этих точках);

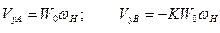. (11.9)

V_уА не зависит от формы деформирования и направлена в сторону вращения генератора; V_уВ зависит от формы деформирования и направлена против вращения генератора.

Точки А и В движутся в противоположных направлениях. В промежутке АВ существует некоторая точка Е, для которой V_уЕ = 0, а V_zЕ имеет максимум. Положение точки Е зависит от формы деформирования (обычно близко к 45⁰). Векторы скоростей изображены на рис.11.4.

Для фрикционной передачи имеют значение только скорости в точках А и А’. Они равны. Скорость V_уА гибкого колеса будет одновременно и окружной скоростью жесткого колеса (без учета проскальзывания).

Точка контакта гибкого и жесткого колес перемещается вместе с генератором и остается в вершине бегущей волны деформирования. При этом окружная скорость ведомого звена (жесткого или гибкого колеса) остается постоянной 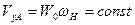. Постоянным будет и передаточное отношение.

Аналогия волновой передачи с простейшей моделью по рис.11.4 состоит в том, что в обоих (деформирования гибкой ленты и гибкого колеса) поперечные или радиальные перемещения сопровождаются продольными или окружными перемещениями. Именно с окружными перемещениями связаны окружные скорости точек гибкого колеса (V_у = du / dt), которые посредством контакта сообщаются жесткому колесу.

Дата добавления: 2014-01-20