Расстановка пределов интегрирования

1.3.1. Прямоугольная область интегрирования

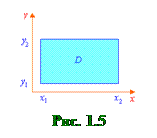При сведении двойных интегралов к повторным, основная трудность возникает при расстановке пределов во внутренних интегралах. Наиболее просто это сделать для прямоугольных областей (см. рис. 1.5).

Пример 1.2. Вычислить двойной интеграл

.

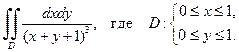Решение. Запишем двойной интеграл в виде повторного:

.

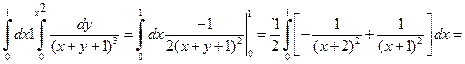
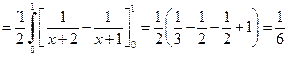1.3.2. Произвольная область интегрирования

Для того, чтобы перейти от двойного интеграла к повторному следует:

1) построить область интегрирования;

2) расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т.е. числами) независимо от того, по какой переменной вычисляется внешний интеграл.

Пример 1.3. Расставить пределы интегрирования в соответствующих повторных интегралах для двойного интеграла

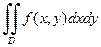, если а) 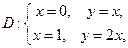б)

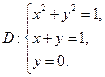
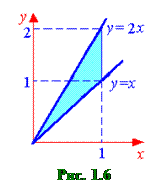Решение. а) Изобразим область интегрирования D (см. рис.1.6). Пусть интегрирование во внешнем интеграле производится по переменной x, а во внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка видно, что x изменяется от 0 до 1, при этом значения переменной y будут изменяться от значений на прямой y=x до значений на прямой y =2 x. Таким образом, получаем

.

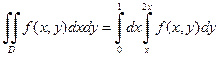Пусть теперь интегрирование во внешнем интеграле производится по y, а во внутреннем – по x. В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x=y /2 и x =1. Это означает, что область интегрирования нужно разбить на две части прямой y =1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x=y /2 до прямой x=y. Во второй области y изменяется от 1 до 2, а x – от прямой x=y /2 до прямой x =1. В результате получим

.

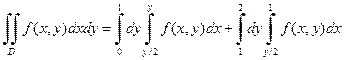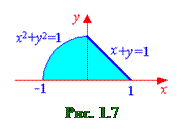б) Построим область интегрирования D (см. рис.1.7). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем – по y. В этом случае при изменении x от –1 до 1 изменения переменной y сверху будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y =0 до 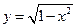; на отрезке [0;1] переменная y изменяется от y =0 до y =1– x. Таким образом,

.

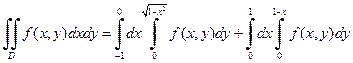Пусть теперь во внешнем интеграле интегрирование производится по y, а во внутреннем – по x. В этом случае y будет изменяться от 0 до 1, а переменная x – от дуги окружности 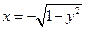до прямой x =1– y. В результате получим

.

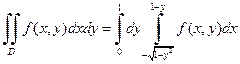Данные примеры показывают, как важно правильно выбирать порядок интегрирования.

Пример 1.4. Изменить порядок интегрирования

а) 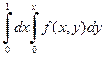; б) .

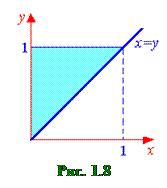Решение. а) Построим область интегрирования. На отрезке [0;1] для x переменная y изменяется от прямой y =0 до прямой y=x. В результате получается следующая область интегрирования (см. рис.1.8). На основании построенного рисунка, расставляем пределы интегрирования

.

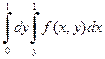б) Построим область интегрирования. На отрезке [0;9/16] для y переменная x изменяется от прямой x = y до параболы 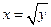; на отрезке [9/16;3/4] – от прямой x = y до прямой x= 3/4. В результате получается следующая область интегрирования (см. рис.1.9). На основании построенного рисунка, расставляем пределы интегрирования,

.

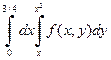Дата добавления: 2014-01-20