Интегрирование элементарных дробей. Элементарными дробяминазываются дроби следующих четырех типов:

Элементарными дробяминазываются дроби следующих четырех типов:

где m, n натуральные числа

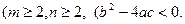
Выясним, как интегрируются элементарные дроби.

Интегралы подстановкой t=ax+b сводятся к табличным интегралам:

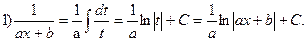(1)

(2)

3) Прежде чем рассмотреть вопрос о нахождении интеграла вида

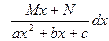рассмотрим частный случай, когда М = 0, N=1,

т. е. рассмотрим интеграл

3),а.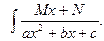

Преобразуем квадратный трехчлен

Тогда данный интеграл можно переписать в следующей форме:

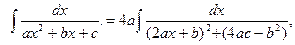
Обозначим 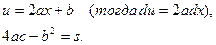(3)

Заметим, что по условию s.0.Тогда

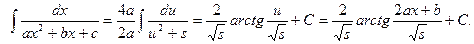
Таким образом, выделением квадрата двучлена интеграл 3, а сводится к табличному интегралу.

Теперь рассмотрим интеграл 3. Сначала преобразуем знаменатель так, как было сделано для частного случая, и применим подстановку (3). Тогда

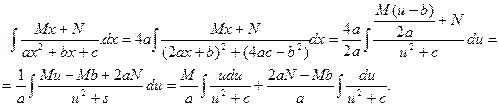
К первому из интегралов применим подстановку

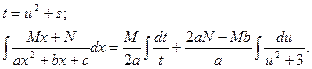
Нахождение интеграла 3 сводится к двум табличным интегралам 2, 4.

Пример 1.

.

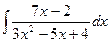Для решения примера 1 нам надо будет в знаменателе выделить квадрат двучлена. Для того чтобы упростить технические выкладки, полезно, если коэффициент при 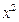не является квадратом целого числа, умножить предварительно числитель и знаменатель на учетверенный коэффициент при 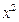(в данном случае на 12):

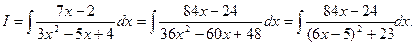
Обозначим 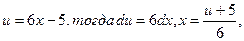и подставим в данный интеграл:

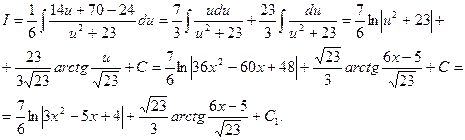
Примечание 1. Если у квадратного трехчлена по определению не является элементарной дробью, однако ее также можно интегрировать предложенным методом.

Пример2. Для решения примера нам надо будет в знаменателе выделить квадрат двучлена.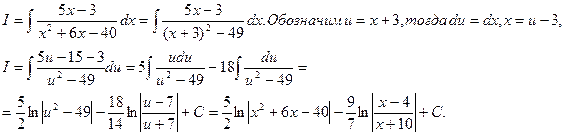

Примечание2. Интегралы от иррациональных функций вида также можно брать методом, аналогичным указанного для интеграла 3.

Пример3.

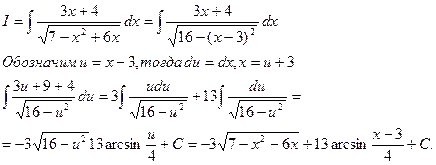
4. Прежде, чем рассмотреть интеграл вида 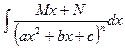, рассмотрим случай, когда M=0, N=1, т.е. интеграл вида .

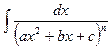Как было, показано, выделением квадрата двучлена и соответствующей заменой квадратный трехчлен 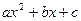может быть выражен через квадратный двучлен .

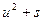Поэтому нахождение интеграла 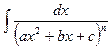сводится к нахождению интеграла . (4)

Преобразуем предварительно интеграл (4)

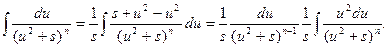(5)

Интеграл 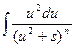будем брать по частям; для этого обозначим

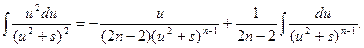(6)

Подставим найденное значение интеграла в равенство (5);

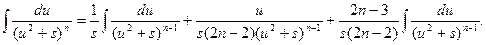(7)

Получившееся равенство позволяет интеграл выразить через интеграл 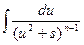, т.е. понизить степень значение знаменателя в подинтегральном выражении на единицу. Применяя формулу (7) последовательно (n-1) раз, приведем к табличному интегралу .

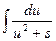Формулу (7) можно применять и тогда, когда 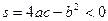. В этом случае указанные преобразования в конечном итоге приведут к табличному интегралу Х: .

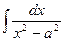Формула (7) называется рекуррентной.

Пример 4. . Применим формулу (7). В данном случае u=x, s=5, n=3.

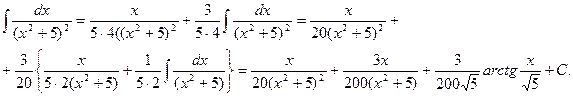
В общем случае интеграл 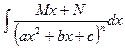берется следующим образом: преобразуют квадратный трехчлен и делают подстановку

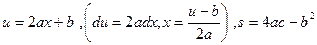. Тогда

В последнем равенстве первый из интегралов подстановкой приводится к табличному интегралу 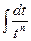, а второй берется по рекуррентной формуле (7).

Пример 5.

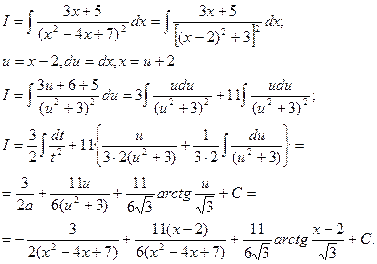
Дата добавления: 2014-01-20