Все деформации витка резьбы и в том числе прогиб витка пропорциональны его нагрузке. Выражая прогиб через относительное перемещение точек A и D (DAD), B и C (DВС) и т.д., где

D_AD = D_A - D_D

D_ВС = D_B - D_C (в)

и учитывая неравенства (а) и (б), находим

D_AD>D_ВС (г)

Следовательно, нагрузка первого витка больше нагрузки второго, и т.д.

Теоретическое решение задачи о распределении нагрузки по виткам резьбы было дано Н.Е. Жуковским в 1902 г. В дальнейшем это решение неоднократно подтверждалось экспериментальными исследованиями на прозрачных моделях. Установлено, например, что при стандартной крепежной гайке с шестью витками первый виток резьбы воспринимает около 52% нагрузки Р, второй – 25%, третий – 12% и последний, шестой виток – только 2% (см. рис.2.15,б).

Указанные теоретические и экспериментальные исследования позволили разработать конструкции специальных гаек, выравнивающих распределение нагрузки в резьбе (рис.2.16,). На рис.2.16,а изображена висячая гайка. Выравнивание нагрузки в резьбе здесь достигают благодаря тому, что винт и гайка имеют однозначные деформации растяжения. При этом неравенство (б) изменится и будет D_D> D_C, а разность между D_AD и D_ВС уменьшится. Кроме того, в наиболее нагруженной нижней зоне висячая гайка обладает повышенной податливостью, что также способствует выравниванию нагрузки а резьбе. При соответствующем подборе формы висячей гайки можно получить равномерное распределение нагрузки в резьбе. На рис.2.16,б показана разновидность висячей гайки – гайка с кольцевой выточкой.

Рис.2.16

У гайки, изображенной на рис.2.16,в, срезаны вершины нижних витков резьбы под углом 15-20⁰. При этом увеличена податливость нижних витков винта, так как они соприкасаются с гайкой не всей поверхностью, а только своими вершинами. Увеличение податливости витков в наиболее нагруженной зоне снижает нагрузку этих витков.

Специальные гайки особенно желательно применять для соединений, подвергающихся действию динамических нагрузок. Разрушение таких соединений, как правило, имеет усталостный характер и происходит в зоне наибольшей концентрации напряжений у нижнего (наиболее нагруженного) витка резьбы. Уменьшение нагрузки нижних витков повышает прочность соединения. Опытом установлено, что применение специальных гаек позволяет повысить динамическую прочность резьбовых соединений на 20-30%.

Расчет резьбы на прочность

Действительный характер распределения нагрузки по виткам гайки, кроме указанных выше причин, зависит от ошибок изготовления и степени износа резьбы, что затрудняет определение истинных напряжений. Поэтому в практике расчет резьбы на прочность производится не по истинным, а по условным напряжениям, которые сравнивают с допускаемыми напряжениями, установленными на основе опыта.

При определении условных напряжений полагают, что все витки резьбы нагружены равномерно (см. рис.2.15,а).

Резьбу принято рассчитывать:

1) по напряжениям смятия на винтовой поверхности (рис.2.17),

2) по напряжениям среза в сечении ab винта или се гайки.

Условия прочности резьбы по напряжениям смятия:

(2.11)

где z=H/S – число витков резьбы в гайке высотой H.

Формула (2.11) является общей для винта и гайки. Вывод формулы прост и не требует дополнительных объяснений. Все элементарные преобразования здесь и в других подобных случаях изучающим рекомендуется производить самим.

Условия прочности резьбы по напряжениям среза:

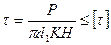для винта,

для гайки, (2.12)

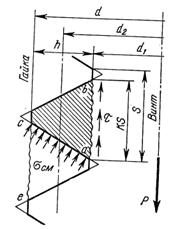Рис.2.17

где K=ab/S или K=ce/S – коэффициент, учитывающий тип резьбы; для треугольной резьбы К» 0,8; для прямоугольной резьбы К=0,5; для трапецеидальной резьбы К=0,65. Если материал винта и гайки одинаков, то по напряжениям среза рассчитывают только винт, так как d>d1 Равнопрочность резьбы и стержня винта является одним из условий назначения высоты стандартных гаек. Так, например, приняв в качестве предельных напряжений пределы текучести материала на растяжение и сдвиг и учитывая, что tт » 0,6sт, запишем условия равнопрочности резьбы на срез и стержня винта на растяжение в виде

(2.13)

откуда при К=0,8 получаем Н» 0,5d₁

здесь 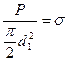- напряжение растяжения в стержне винта, рассчитанное приближенно по внутреннему диаметру резьбы d₁.

Учитывая сложность напряженного состояния резьбы, а также предусматривая ослабление резьбы от истирания и возможных повреждений при завинчивании, высоту стандартных гаек крепежных изделий принимают

Н» 0,8d

По тем же соображениям устанавливают нормы на глубину завинчивания винтов и шпилек в детали:

В стальные детали Н₁ » d, в чугунные и силуминовые Н₁ » 1,5d.

При этом прочность резьбы превышает прочность стержня.

Стандартная высота гайки и глубины завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей.

Расчет на прочность стержня винта (болта)

Дата добавления: 2014-01-20