Определение и вычисление тройного интеграла

Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных.

Определение: Пусть в некоторой замкнутой ограниченной области 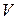трехмерного пространства задана ограниченная функция 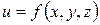. Разобьем область 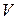на 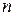произвольных областей, не имеющих общих внутренних точек с объемами 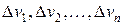. В каждой области возьмем производную точку 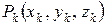и составим сумму: 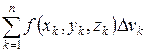, которая называется интегральной суммой для функции 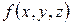по области 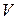. Перейдем к пределу в этой сумме при 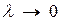, где 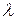– наибольший из диаметров частичных областей 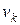. Если этот предел существует и конечен, и не зависит ни от способа разбиения области 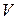, ни от выбора точек 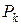, то этот предел называется тройным интегралом функции 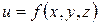по области 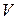и обозначается:

.

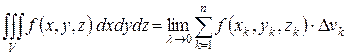В этом случае функция 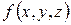называется интегрируемой в области 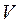; 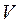- областью интегрирования; , 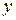и 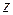- переменными интегрирования.

Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства. Они обладают аналогичными двойным интегралам необходимыми и достаточными условиями существования и свойствами. Если положить всюду в области 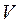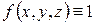, то из определения тройного интеграла следует формула для вычисления объема тела :

.

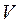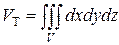Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Рассмотрим область 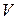ограниченную снизу и сверху поверхностям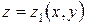и и 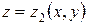, а с боковых сторон цилиндрической поверхностью, и пусть область 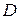– проекция области 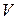на плоскость 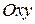, в которой определены и непрерывны функци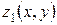и и 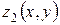(см. рисунок 1). Предположим что каждая прямая, параллельная оси 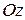, пересекает границу области 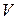не более чем в двух точках.

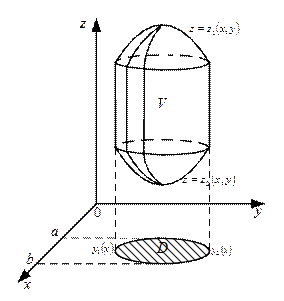
Рисунок 1

Тогда для любой функции 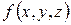, непрерывной в области 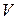, имеет место формула:

,

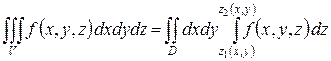позволяющая свести вычисление тройного интеграла к последовательному вычислению внутреннего определенного интеграла по переменной 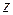(при постоянных и 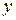) и внешнего двойного интеграла по области .

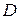Переходя от двойного интеграла к повторному, получаем формулу:

,

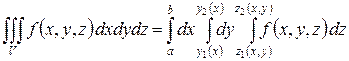(1)

сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим, то есть переменные , 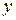и 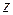в формуле (1) можно менять ролями.

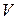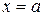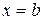
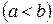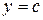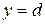
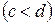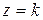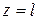
В частности, если – параллелепипед с гранями , , , , , , 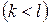то формула (1) принимает вид:

.

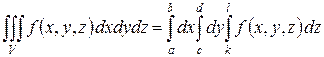(2)

В этом случае интегрирование можно проводить в любом порядке.

Пример 1. Вычислить интеграл: 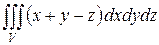, где 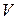– параллелепипед, ограниченный плоскостями: 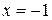, , 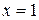, , 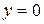, 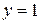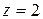(см. рисунок 2).

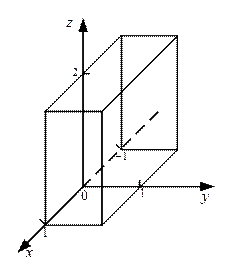
Рисунок 2

Решение:

.

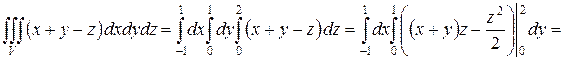
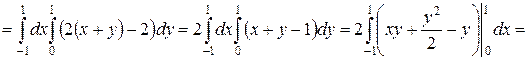
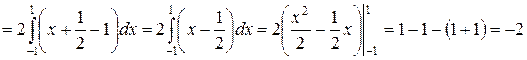Ответ: .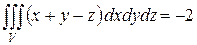

Пример 2. Вычислить интеграл 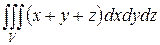, где 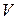– пирамида, ограниченная плоскостью 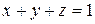и координатными плоскостями , , .

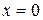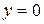Решение: область 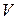проектируется на плоскость 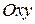в треугольник 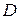, ограниченный прямыми 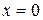, , 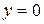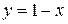(см. рисунок 3).

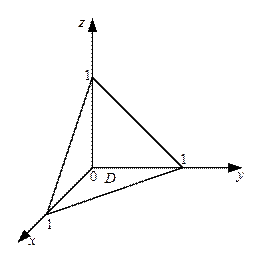
Рисунок 3

.

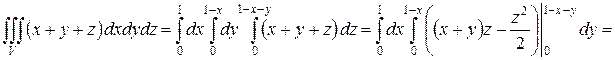
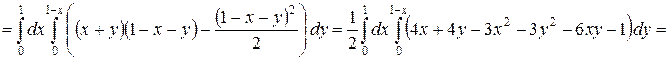
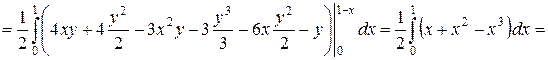
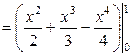
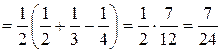Ответ: .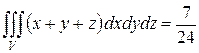

Дата добавления: 2014-01-20