Замена переменных в тройном интеграле

Как для двойных интегралов, так и для тройных имеют место формулы перехода от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сферические координаты.

Замену переменных в тройном интеграле производят по следующему правилу.

Если ограниченная замкнутая область 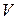пространства 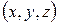взаимно однозначно отображается на область 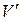пространства 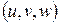с помощью непрерывно дифференцируемых функций 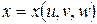, , 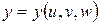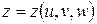и определитель 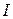в области 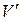не обращается в ноль:

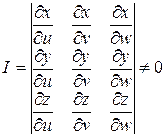, то справедлива формула:

.

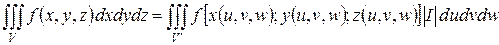В частности, при переходе от прямоугольных координат , 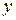и 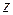к цилиндрическим координатами 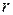, , 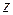связанным с , 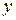и 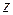формулами:

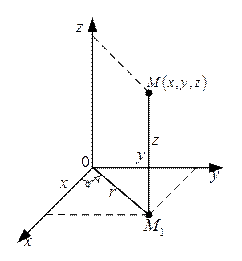
Рисунок 4

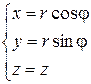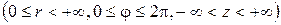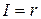, , , поэтому

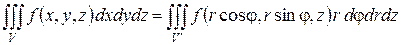
(1)

Название “цилиндрические координаты” связано с тем, что координатная поверхность 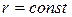(то есть поверхность, все точки которой имеют одну и ту же координату 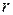) является цилиндром, прямолинейные образующие которого параллельны оси .

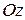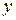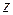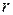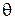При переходе от прямоугольных координат , и к сферическим координатам , и связанным с , 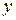и 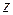формулами:

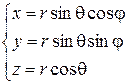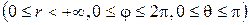, , , поэтому

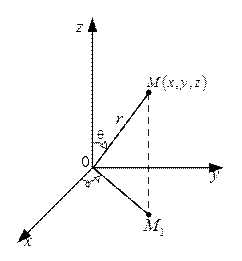
Рисунок 5

(2)

Название «сферические координаты» связано с тем, что координатная поверхность 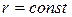(то есть поверхность, все точки которой имеют одну и ту же координату 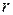) является сферой. Сферические координаты иначе называют полярными координатами в пространстве.

При вычислении тройного интеграла путем перехода к цилиндрическим или сферическим координатам область 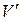обычно не изображают, а пределы интегрирования расставляют непосредственно по виду области 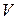, используя геометрический смысл новых координат.

Пример 1. Вычислить интеграл: ,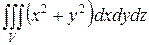

где 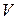- область ограниченная поверхностям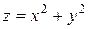и и 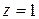(см. рисунок 6).

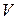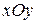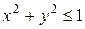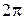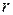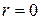Решение: перейдем к цилиндрическим координатам, область проектируется на плоскость в круг , при этом изменятся в пределах от до , координата -от до .

Рисунок 6

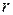
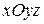Постоянному значению в пространстве соответствует цилиндр 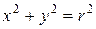. Рассматривая пересечение этого цилиндра с областью 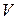, получаем изменение координаты 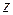от значений для точек, лежащих на параболе 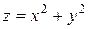до значений для точек, лежащих на плоскости 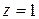, то есть от 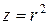до 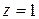. Применяя формулу (1) имеем:

.

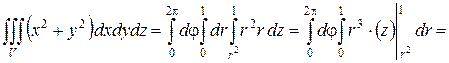
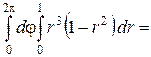
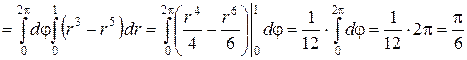Ответ: .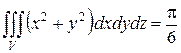

Трудно дать какую-либо общую рекомендацию, когда следует применить ту или иную схему координат это зависит и от области интегрирования, и от вида подынтегральной функции. Однако, например, формулой (2) удобнее пользоваться, когда 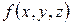имеет вид , а также когда область 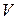является шар 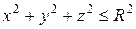или его часть.

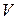Пример 2. Вычислить интеграл: , где - шар .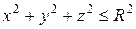

Решение: перейдем к сферическим координатам:

, .

.

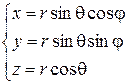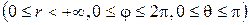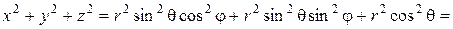
По формуле (2) получаем:

.

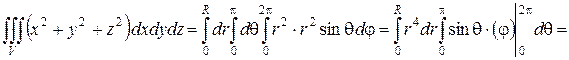
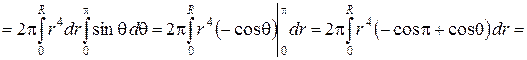
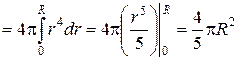Ответ: .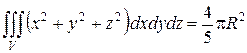

Дата добавления: 2014-01-20