
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства определённого интеграла
|
|
|
|
При вычислении, исследовании определённого интеграла могут пригодиться следующие свойства определённого интеграла:

| Переменную интегрирования можно обозначать любой буквой. | (5.1) |

| Если переставить пределы интегрирования, интеграл умножится на -1. | (5.2) |
 
| Интеграл от суммы (разности) равен сумме (разности) интегралов. | (5.3) |
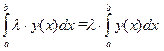
| Постоянный множитель можно вынести за знак интеграла. | (5.4) |
 
| Свойство аддитивности, или сложения. | (5.5) |
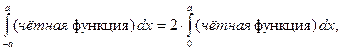
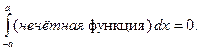
| (5.6) |
¨ Свойства (5.1) – (5.5) вытекают из соответствующих свойств знака двойной подстановки. В качестве примера докажем формулу (5.5):
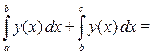
 = (3.6) =
= (3.6) =
Докажем равенства (5.6). Если 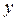 – чётная функция (рис. 5.1), то
– чётная функция (рис. 5.1), то
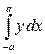 =│Фигура симметрична относительно оси
=│Фигура симметрична относительно оси 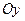 │=
│= 
Если же 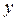 – нечётная функция (рис. 5.2), то
– нечётная функция (рис. 5.2), то
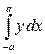 =│Фигура симметрична относительно точки
=│Фигура симметрична относительно точки  │=
│= 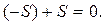 ■
■
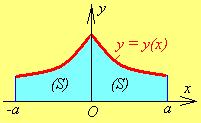

Рис. 5.1 Рис. 5.2
Примеры: 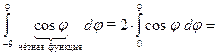
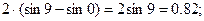

Тренировка по теме «Свойства определённого интеграла»
Найдите интегралы.
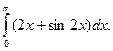
1)  2)
2) 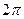 3)
3)  4)
4)  5)
5) 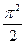
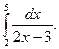
1) 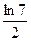 2)
2) 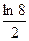 3)
3) 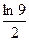 4)
4)  5)
5) 

1)  2)
2)  3)
3)  4)
4)  5)
5) 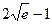
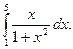
1)  2)
2)  3)
3) 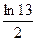 4)
4) 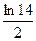 5)
5) 
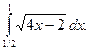
1)  2)
2) 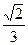 3)
3) 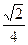 4)
4) 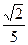 5)
5) 
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 373; Нарушение авторских прав?; Мы поможем в написании вашей работы!