ЛЕКЦИЯ 2. Интеграл от разрывной функции (несобственный интеграл II рода)

Интеграл от разрывной функции (несобственный интеграл II рода)

Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)

Определение: Пусть функция непрерывна на промежутке 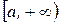. Если существует конечный предел , то его называют несобственным интегралом первого рода и обозначают .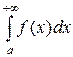

Таким образом, по определению

=.

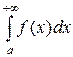В этом случае говорят, что несобственный интеграл 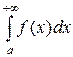сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интеграл 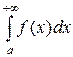расходится.

Аналогично определяется несобственный интеграл на промежутке :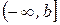

=.

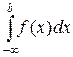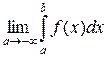Несобственный интеграл с двумя бесконечными пределами определяется формулой

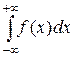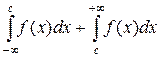=, где с – произвольное число.

В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функция 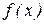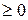на промежутке 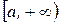и интеграл 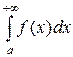сходится, то он выражает площадь бесконечно длинной криволинейной трапеции (см. рисунок 1).

Рисунок 1

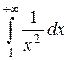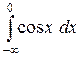Пример. Вычислить несобственные интегралы или установить их расходимость: 1) ; 2) ; 3) .

Решение: 1) , интеграл сходится;

2) 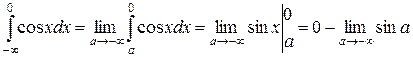, интеграл расходится, так как при предел не существует.

3) 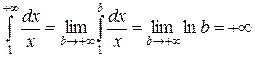, интеграл расходится.

В некоторых задачах нет необходимости вычислить интеграл; достаточно лишь знать, сходится ли он или нет.

Приведем без доказательства некоторые признаки сходимости.

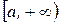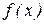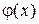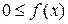
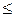
Теорема 1 (I признак сравнения). Если на промежутке непрерывные функции и удовлетворяют условию 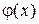, то из сходимости интеграла 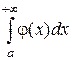следует сходимость интеграла 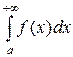, а из расходимости интеграла следует расходимость интеграла .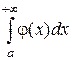

Пример. Сходится ли интеграл ?

Решение: При имеем 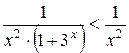. Но интеграл сходится. Следовательно, интеграл 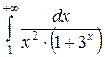также сходится (и его значение меньше 1).

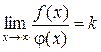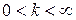
Теорема 2 (II второй признак сравнения). Если существует предел , , 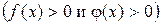то интегралы 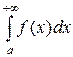и 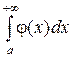одновременно оба сходятся или оба расходятся (т.е. ведут себя одинаково в смысле сходимости).

Пример. Исследовать сходимость интеграла сходится, так как сходится и

.

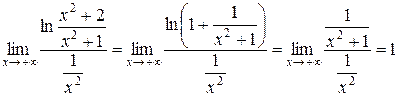Определение: Пусть функция непрерывна на промежутке и имеет бесконечный разрыв при 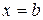(см. рисунок 2). Если существует конечный предел 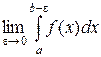, то его называют несобственным интегралом второго рода и обозначают .

Таким образом, по определению,

=.

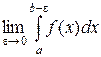Если предел в правой части существует и конечен, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится.

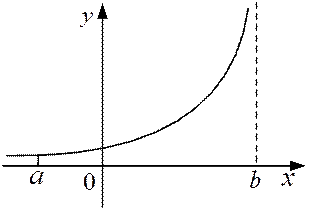
Рисунок 2

Аналогично, если функция терпит бесконечный разрыв в точке 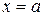, то полагают

=(см. рисунок 3).

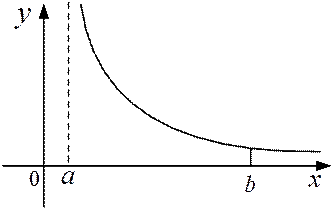
Рисунок 3

Если функция терпит разрыв во внутренней точке отрезка (см. рисунок 4), то несобственный интеграл второго рода определяется формулой

.

В этом случае интеграл называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

Рисунок 4

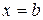В случае, когда , несобственный интеграл второго рода (разрыв в точке ) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции (см. рисунок 2).

Рисунок 2

Пример. Вычислить .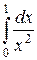

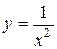Решение: При функция терпит бесконечный разрыв;

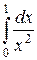
, интеграл расходится.

Сформулируем признаки сходимости для несобственных интегралов второго рода.

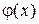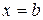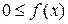
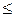
Теорема 1 (I признак сравнения). Если на промежутке функции и непрерывны, при терпят бесконечный разрыв и удовлетворяют условию 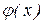. Из сходимости интеграла вытекает сходимость интеграла , а из расходимости интеграла вытекает расходимость интеграла .

Теорема 2 (II признак сравнения). Пусть функции и 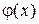непрерывны на промежутке и в точке 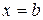терпят бесконечный разрыв. Если существует предел 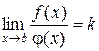, , 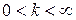то интегралы и одновременно сходятся или расходятся.

Пример. Сходится ли интеграл ?

Решение: Функция имеет на единственный разрыв в точке . Рассмотрим функцию . Интеграл

расходится. И так как

,

то интеграл также расходится.

Замена переменных в двойном интеграле. Определитель Якоби. Вычисление двойных интегралов в полярной системе координат. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур, объемов тел.

Дата добавления: 2014-01-20