Косвенные измере­ния при нелинейной зависимости между аргументами

­

Для об­работки результатов измерений при нелинейных зависимостях между аргументами и некоррелированных погрешностях используется метод линеари­зации. Он состоит в том, что нелинейная функция, связывающая измеряемую величину с аргументами, разлагается в ряд Тейлора:

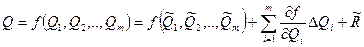(9.4)

Здесь f/Q_i – первая частная производная от функции f по аргу­менту Q_i, вычисленная в точке – отклонение результата измерения аргумента ΔQ_i от его среднего арифметиче­ского; 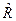– остаточный член:

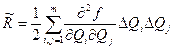
Метод линеаризации применим, если остаточным членом мож­но пренебречь. Это возможно в том случае, если

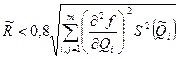
где S(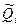) – СКО случайной погрешности результата измерений аргумента Q_i. При необходимости результаты косвенных измере­ний можно уточнить, используя члены ряда Тейлора более высо­кого порядка. Оценка результата определяется по формуле

(9.5)

Абсолютная погрешность косвенного измерения Δ=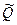–Q, как это следует из уравнения (9.4), равна

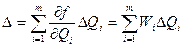
где W_i = f/Q_i – коэффициенты влияния i-го аргумента; ΔQ_i – абсолютная погрешность измерения i -го аргумента; W_iΔQ_i – частная i -я погрешность определения результата косвенного из­мерения.

Пример 9.1. Разложить в ряд Тейлора уравнение для определения плот­ности и получить выражение для расчета абсолютной погрешности.

Плотность твердого тела ρ определяется как отношение результата из­мерения его массы m к объему V. При этом в соответствии с (9.4) получаем выражение

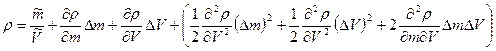
где в скобках стоит остаточный член. Учитывая, что

; ;; ; .

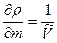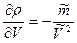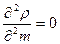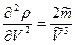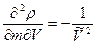окончательно получим

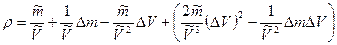
Абсолютная погрешность

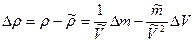
Коэффициенты влияния чаще всего определяются путем под­становки в выражения для частных производных оценок 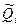. По­этому вместо самих коэффициентов влияния получаются их оцен­ки. В ряде случаев они устанавливаются экспериментально, что приводит к возникновению еще одной погрешности нелинейных косвенных измерений. Этой погрешности можно избежать, если зависимость (9.1) имеет вид

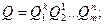(9.6)

Тогда коэффициенты влияния

…

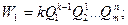
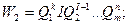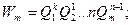
Оценка измеряемой величины находится по (8.6), (8.7), а ее отно­сительная погрешность с учетом последних формул определяется как

Из полученной формулы видно, что коэффициенты влияния для относительной погрешности оказываются равными показателям сте­пеней соответствующих аргументов. Последние известны точно, и отмеченная выше погрешность не возникает. Для рассмотренного выше примера измерения плотности тела имеем δρ = δm – δV.

Оценка СКО случайной погрешности результата косвенного из­мерения

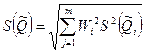(9.7)

При точно известных коэффициентах влияния оно совпадает с уравнением (9.2), полученным для линейных косвенных измере­ний. Для зависимости вида (9.6) данная оценка, представленная в относительной форме, запишется в виде

где 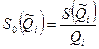– оценка СКО i-го аргумента, представленная в относительной форме.

Доверительные границы случайной погрешности результата при нормально распределенных погрешностях измерений аргументов вычисляются так же, как и для линейных косвенных измерений, при условии, что вместо коэффициентов b_i в формулах подставля­ются коэффициенты влияния W_i. Аналогичным образом поступа­ют при определении границ неисключенной систематической по­грешности. Погрешность результата нелинейных косвенных измерений оценивается так же, как и при линейных измерениях.

Дата добавления: 2014-01-20