Совместные и совокупные измерения

Эти виды измерений характеризуются тем, что значения иско­мых величин рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами, определяемыми посредством прямых или косвенных измерений. При этом измеряются не­сколько комбинаций значений указанных величин. Каждая такая комбинация позволяет получить одно уравнение, а система содер­жит всю информацию о значениях искомых величин и имеет вид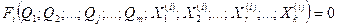

где Р_i – символ функциональной зависимости между величина­ми в i-м опыте; i =1; 2;...; n; n – число опытов; Q_i – значения искомых величин, общее число которых равно m; 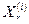– получен­ные в i-м опыте значения k величин, измеряемых прямыми или косвенными методами.

Если Q_j являются значениями одной и той же величины, то измерения называются совокупными, если разных физических ве­личин, – то совместными.

После подстановки в исходную систему уравнений результатов 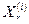прямых или косвенных измерений и проведения необходимых преобразований получим n уравнений, содержащих лишь иско­мые величины я числовые коэффициенты: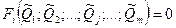

Такие уравнения называют условными.

Для того чтобы рассчитать значения искомых величин, доста­точно иметь m уравнений, т.е. столько же, сколько содержится неизвестных. Тогда результаты измерений и доверительные грани­цы их погрешностей можно найти методами обработки результатов косвенных измерений. Однако обыкновенно для уменьшения погреш­ностей результатов измерений делается значительно больше изме­рений, чем это необходимо для определения неизвестных, т.е. n>m.

Вследствие ограниченной точности определения величин Х_r ус­ловные уравнения одновременно не обращаются в тождества, ни при каких значениях искомых величин. И поскольку найти истинные значения искомых величин невозможно, то задача сводится к нахо­ждению их оценок, представляющих собой наилучшие приближе­ния к истинным значениям. Предположим, что 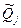, где j = 1, 2,..., m, наилучшие приближения к неизвестным Q_j. Если значения этих оценок подставить в условные уравнения, то их правые части будут отличаться от левых. Для получения тождеств нужно записать:

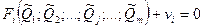(9.8)

где v_i – величины, называемые остаточными погрешностями ус­ловных уравнений. Если в систему условных уравнений подста­вить истинные значения искомых величин, то остаточные погреш­ности превратятся в случайные погрешности условных уравнений. Одним из наиболее общих способов отыскания оценок истин­ных значений измеряемых величин является регрессионный ана­лиз, или, как его часто называют, метод наименьших квадратов. Согласно ему оценки 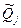выбираются так, чтобы минимизировать сумму квадратов остаточных погрешностей условных уравнений. Сумма квадратов остаточных погрешностей, определенных в соот­ветствии с системой условных уравнений (9.8), составляет

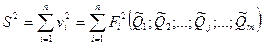
и достигает минимума при системе значений Q_j обращающей в нуль все частные производные от S₂ по искомым величинам: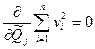

Выражая остаточные погрешности через функции, стоящие в левой части условных уравнений, получаем систему из m уравне­ний с m неизвестными: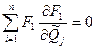

где j = 1, 2,..., m, которая может быть решена относительно оценок 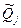. искомых величин.

При решении задачи в общем случае, когда условные уравнения не линейны, а результаты отдельных измерений коррелированны, иногда возникает ряд непреодолимых трудностей. Задача от­носительно несложно решается лишь тогда, когда условные уравнения линейны или приведены к линейным известными спо­собами и при отсутствии корреляции между результатами отдель­ных наблюдений. Оценки, даваемые методом наименьших квадратов, являются состоятельными и несмещенными, а при нормальном распределе­нии результатов измерений и эффективными.

Дата добавления: 2014-01-20