
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм методов
|
|
|
|
| Метод сравнения коэффициентов | Метод отдельных значений коэффициентов | |
Приведем к общему знаменателю слагаемые правой части разложения; получим тождество 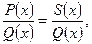 где где 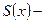 многочлен с неопределенными коэффициентами; многочлен с неопределенными коэффициентами;
| ||
Приравняем числители 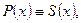 т.к. знаменатели равны; т.к. знаменатели равны;
| ||
Приравняем коэффициенты при одинаковых степенях  Получим СЛАУ, из которой найдем искомые коэффициенты. Получим СЛАУ, из которой найдем искомые коэффициенты.
| Придадим 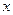 конкретные значения столько раз, сколько неопределенных коэффициентов (обычно вместо конкретные значения столько раз, сколько неопределенных коэффициентов (обычно вместо 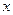 полагают значения действительных корней многочлена полагают значения действительных корней многочлена 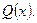
|
Пример. Разложить дробь на простейшие 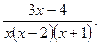
Решение. По теореме разложим дробь на простейшие: 
Найдем коэффициенты «методом отдельных значений коэффициентов»:
1) 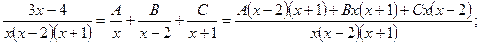
2) 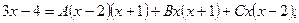
3) Пусть 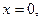 тогда
тогда 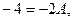 т.е.
т.е. 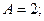
Пусть  тогда
тогда 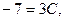 т.е.
т.е. 
Пусть 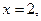 тогда
тогда 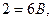 т.е.
т.е. 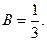
Следовательно, 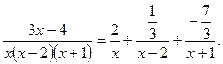
Интегрирование простейших дробей
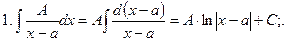
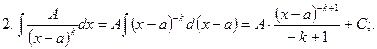
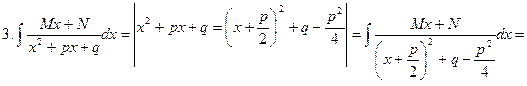
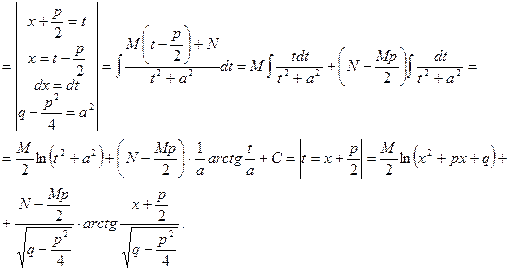
Правило интегрирования рациональных дробей 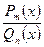
1. Выделяем целую часть, если дробь неправильная.
2. Находим нули знаменателя 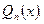
3. Разлагаем знаменатель 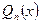 на линейные множители, соответствующие действительным корням и квадратные трехчлены, соответствующие комплексным корням.
на линейные множители, соответствующие действительным корням и квадратные трехчлены, соответствующие комплексным корням.
4. Разлагаем правильную дробь на сумму простейших дробей.
5. Интегрируем целую часть (если она есть) и простейшие дроби.
6. Складываем полученные интегралы.
Пример.. Вычислить интеграл 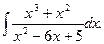
Решение. 1) Выделим целую часть данной неправильной дроби
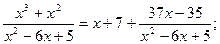
2) Разложим знаменатель на линейные множители по формуле 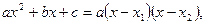 где
где 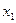 и
и 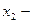 корни квадратного уравнения, то есть
корни квадратного уравнения, то есть
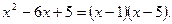
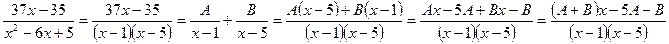 Найдем
Найдем 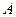 и
и 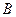 «методом сравнения коэффициентов»:
«методом сравнения коэффициентов»:
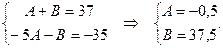
Значит, разложение правильной дроби в виде суммы простейших дробей имеет вид:
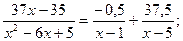
3) 
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 729; Нарушение авторских прав?; Мы поможем в написании вашей работы!