Задачи, приводящие к понятию определенного интеграла. Лекция 8.3. Определенный интеграл и его вычисление

Лекция 8.3. Определенный интеграл и его вычисление

План:

1. Задачи, приводящие к понятию определенного интеграла.

2. Понятие определенного интеграла и его свойства.

3. Формула Ньютона-Лейбница и основные методы нахождения определенного интеграла.

Интегралы, рассмотренные ранее, носили название неопределенных. Само название указывает, что в нем какая-то величина должна быть неопределенна. И это постоянная С, которая могла принимать любое числовое значении.

Определенному интегралу в математическом анализе отводится особое место в связи с его практической значимостью. Так, к вычислению определенного интеграла сводится решение задач по нахождению площадей, длин и объемов тел, работы, скорости движущего тела и т.д.

Существенное отличие определенного интеграла от неопределенного заключается в том, что определенный интеграл выражается некоторым числом. Однако между этими интегралами есть много общего.

Задача о массе стержня

Зная длину стержня 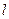и его плотность 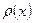для любого 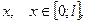найти его массу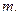

Решение. Если стержень однородный, то есть 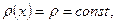то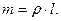

Пусть стержень неоднородный, т.е. 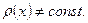Выполним следующие действия:

1) Разобьем стержень точками

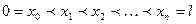
на n произвольных частичных отрезков

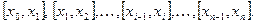
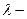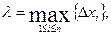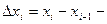Означим через длину наибольшего частичного отрезка разбиения: где длина 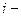го отрезка.

2) В каждом из полученных частичных отрезков выберем произвольную точку 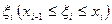и положим, что на отрезке 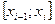плотность постоянна и равна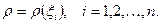

3) Массу 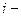го отрезка 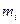вычислим приближенно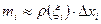

4) Тогда масса всего стержня приближенно равна

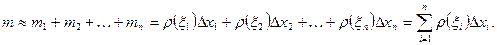
Это приближенное равенство тем точнее, чем меньше значение 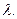Будем производить разбиение стержня на части таким образом, чтобы 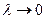(а тогда 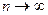). Тогда

Задача о пройденном пути

Зная промежуток времени от 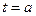до 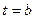и функцию скорости движения 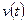точки 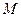в момент времени 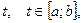найти путь 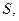пройденный точкой M.

Решение. Если бы точка M двигалась равномерно, то есть 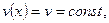то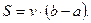

Пусть движение неравномерное и скорость есть непрерывная функция, т.е. 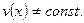Выполним следующие действия:

1) Разобьем промежуток времени точками

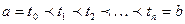
на n произвольных частичных отрезков

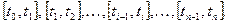
Означим через 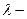длину наибольшего частичного отрезка разбиения:

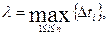где длина 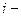го отрезка.

2) В каждом из полученных частичных отрезков выберем произвольную точку 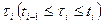и будем считать, что за этот промежуток времени 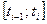происходит равномерное движение со скоростью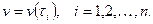

3) Путь 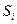, пройденный точкой M за промежуток времени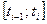приближенно равен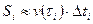

4) Тогда путь S, пройденный за время от 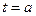до 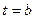приближенно равен

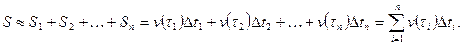
Это приближенное равенство тем точнее, чем меньше 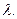Устремляя 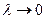(а тогда 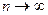), в пределе получим

Дата добавления: 2014-01-20