
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие определенного интеграла и его свойства
|
|
|
|
Пусть на отрезке 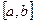 задана непрерывная функция
задана непрерывная функция  причем для определенности
причем для определенности 
1) Разобьем отрезок 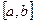 на оси
на оси 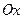 точками
точками
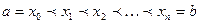
на n произвольных частичных отрезков
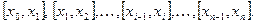
Означим через 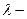 длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения: 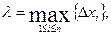 где
где 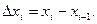
2) В каждом из полученных частичных отрезков выберем произвольную точку 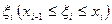 и
и
3) составим сумму 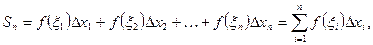
Данная сумма называется интегральной суммой для функции 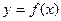 на отрезке
на отрезке 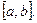
4) Если существует конечный предел I интегральной суммы при 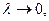 не зависящий ни от способа разбиения отрезка
не зависящий ни от способа разбиения отрезка 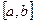 , ни от выбора точек
, ни от выбора точек 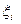 внутри каждого отрезка, то этот предел называют определенным интегралом от функции
внутри каждого отрезка, то этот предел называют определенным интегралом от функции 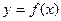 по отрезку
по отрезку 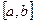 и обозначается:
и обозначается:
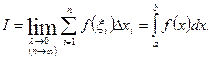
Функция  называется подынтегральной функцией, выражение
называется подынтегральной функцией, выражение  подынтегральным выражением, числа
подынтегральным выражением, числа  и
и 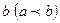 называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования, 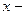 переменной интегрирования.
переменной интегрирования.
Теорема 1. Если функция 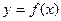 непрерывна на отрезке
непрерывна на отрезке 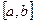 , то она интегрируема на нем.
, то она интегрируема на нем.
Теорема 2. Если функция 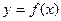 кусочно-непрерывна на отрезке
кусочно-непрерывна на отрезке 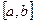 , то она интегрируема на нем.
, то она интегрируема на нем.
Таким образом, возвращаясь к рассмотренным выше задачам, получаем:
- масса неоднородного стержня длины l вычисляется по формуле
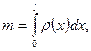
где 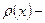 функция плотности;
функция плотности;
- путь, пройденный неравномерно двигающейся точкой за время от 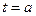 до
до 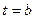 вычисляется по формуле
вычисляется по формуле
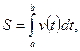
где  функция скорости.
функция скорости.
Геометрическая интерпретация определенного интеграла
Пусть на отрезке 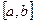 задана непрерывная функция
задана непрерывная функция 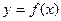 , причем
, причем 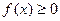 на
на 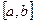 .
.
Криволинейной трапецией называется фигура, ограниченная осью 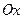 , прямыми
, прямыми  и графиком функции
и графиком функции 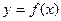 .
.
Найдем площадь криволинейной трапеции.
1) Разобьем отрезок 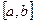 на оси
на оси 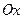 точками
точками

на n произвольных частичных отрезков 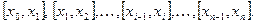
Означим через 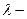 длину наибольшего частичного отрезка разбиения:
длину наибольшего частичного отрезка разбиения: 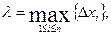 где
где 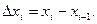
2) В каждом из полученных частичных отрезков выберем произвольную точку 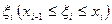 и
и
3) составим сумму 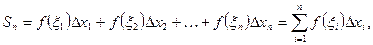
Интегральная сумма 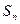 равна площади ступенчатой фигуры, состоящей из прямоугольников, вписанных в криволинейную трапецию (рис. 36)
равна площади ступенчатой фигуры, состоящей из прямоугольников, вписанных в криволинейную трапецию (рис. 36)
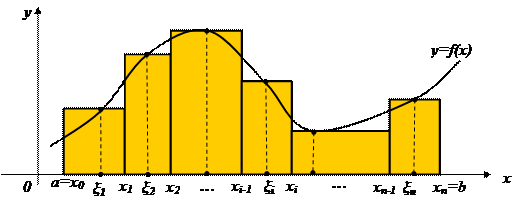
Рис. 36
Площадью криволинейной трапеции считают предел площадей ступенчатых фигур, получаемых при неограниченном увеличении n числа точек дробления отрезка 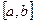 и при условии, что
и при условии, что 
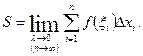
Таким образом, геометрически интеграл от непрерывной неотрицательной на отрезке 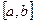 функции
функции 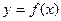 есть площадь криволинейной трапеции, ограниченной линиями
есть площадь криволинейной трапеции, ограниченной линиями  осью
осью 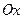 и графиком функции
и графиком функции 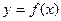 :
:
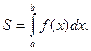
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла, другие справедливы только для него.
Основные свойства определенного интеграла
Будем считать, что функция 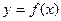 непрерывна на
непрерывна на 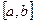 .
.
1. Интеграл с одинаковыми пределами интегрирования равен нулю:
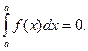
2. 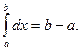
3. При перестановке местами пределов интегрирования определенный интеграл меняет свой знак на противоположный: 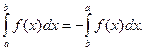
4. Интеграл по отрезку равен сумме интегралов по его частям, т.е. имеет место равенство: 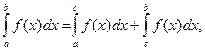 если
если 
5. Постоянный множитель можно выносить за знак определенного интеграла: 
6. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых, т.е. (для двух функций):

7. Теорема о среднем. Если 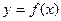 непрерывна на
непрерывна на 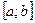 , то существует такое число
, то существует такое число 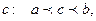 что
что 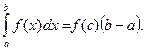
8. Определенный интеграл зависит только от вида функции 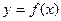 и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой:
и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой:
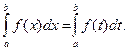
Вычисление определенного интеграла как предела интегральной суммы неудобно и трудоемко. Поэтому целесообразно указать более удобный и эффективный способ вычисления определенного интеграла. Основан он на связи неопределенного и определенного интеграла и выражается в формуле Ньютона-Лейбница.
3. Формула Ньютона – Лейбница и основные методы нахождения определенного интеграла
Теорема. Если 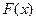 есть первообразная для непрерывной на отрезке
есть первообразная для непрерывной на отрезке 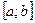 функции
функции 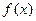 , то справедлива формула
, то справедлива формула 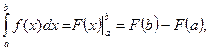
т.е. определенный интеграл от непрерывной функции равен разности значений первообразной от верхнего и нижнего пределов интегрирования.
Данное равенство называют формулой Ньютона-Лейбница.
Итак, задача вычисления определенного интеграла сводиться в первую очередь к задаче нахождения неопределенного интеграла, а, следовательно, основана на использовании свойств, таблиц и методов, приведенных для неопределенного интеграла.
Пример
а) 
б) 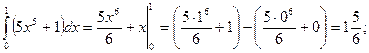
в) 
Тесная связь между определенным и неопределенным интегралом позволяет сделать вывод о том, что при вычислении определенного интеграла можно пользоваться теми же методами интегрирования. Но существуют и особенности при использовании этих методов для определенных интегралов.
Метод интегрирования по частям в определенном интеграле
Пусть функции  и
и 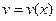 имеют непрерывные производные на промежутке
имеют непрерывные производные на промежутке 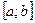 . Тогда, справедлива следующая формула:
. Тогда, справедлива следующая формула:
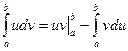
Эта формула называется формулой интегрирования по частям в определенном интеграле.
Пример 8.10. Вычислить интеграл 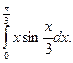
Решение. 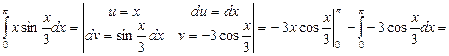
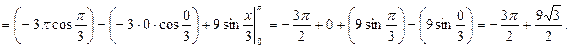
Метод замены переменной в определенном интеграле
Метод замены переменной в определенном интеграле основан на следующей теореме.
Теорема 8.6. Пусть 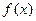 непрерывна на отрезке
непрерывна на отрезке 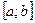 и пусть
и пусть
1) функция  монотонна, непрерывна и имеет непрерывную производную, когда t меняется от
монотонна, непрерывна и имеет непрерывную производную, когда t меняется от 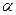 до
до 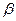 ;
;
2)  и
и 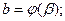
тогда справедлива формула 
Даная формула называется формулой замены переменной в определенном интеграле.
Из формулы видно, что при замене переменной в определенном интеграле подынтегральное выражение преобразуется так же, как и в неопределенном, но при этом в отличие от неопределенного интеграла преобразуются и пределы интегрирования.
Замечание 1. В практике интегрирования применяются подстановки вида  , т.е. новая переменная интегрирования вводится как некоторая функция переменной х, а новые пределы интегрирования определяются из формул:
, т.е. новая переменная интегрирования вводится как некоторая функция переменной х, а новые пределы интегрирования определяются из формул:  и
и 
Замечание 2. При нахождении определенного интеграла методом замены переменной нет необходимости возвращаться к старой переменной.
Пример 8.11. Вычислить интеграл
Решение.
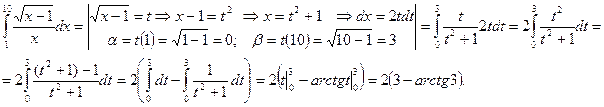
Лекция 8.4. Приложения определенного интеграла
План:
1. Понятие несобственного интеграла первого рода и его нахождение.
2. Понятие несобственного интеграла второго рода.
3. Приложения определенного интеграла.
Определяя понятие определенного интеграла, как предела интегральных сумм, предполагалось, что 1) отрезок интегрирования конечный; 2) подынтегральная функция непрерывна на этом отрезке. Если, хотя бы одно из условий не выполнено, то данное определение теряет смысл. Так, в случае бесконечного отрезка интегрирования, нельзя разбить отрезок на 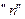 частей конечной длины, а в случае разрывной функции интегральная сумма не имеет конечного предела. Тогда и появляется понятие несобственного интеграла первого рода и несобственного интеграла второго рода.
частей конечной длины, а в случае разрывной функции интегральная сумма не имеет конечного предела. Тогда и появляется понятие несобственного интеграла первого рода и несобственного интеграла второго рода.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1030; Нарушение авторских прав?; Мы поможем в написании вашей работы!