
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отличительные особенности восточных оздоровительных систем
|
|
|
|
Приложения определенного интеграла
Рассмотрим несколько основных приложений определенного интеграла.
Вычисление площади плоской фигуры в декартовой системе координат
| № | Рисунок | Формула |
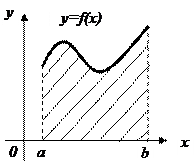 Криволинейная трапеция ограничена сверху графиком функции
Криволинейная трапеция ограничена сверху графиком функции 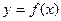 , снизу осью , снизу осью 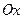 , слева и справа прямыми , слева и справа прямыми  и и 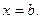
| 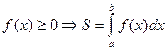
| |
Криволинейная трапеция ограничена снизу графиком функции 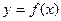 , сверху осью , сверху осью 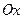 , слева и справа прямыми , слева и справа прямыми  и и 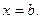

| 
| |
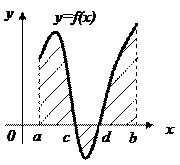 Криволинейная трапеция ограничена кривой Криволинейная трапеция ограничена кривой 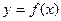 , которая конечное число раз меняет знак на , которая конечное число раз меняет знак на 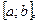 осью осью 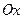 и прямыми и прямыми  и и 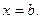
| 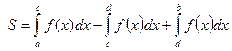
| |
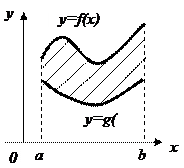 Криволинейная трапеция ограничена сверху графиком функции Криволинейная трапеция ограничена сверху графиком функции 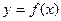 , снизу графиком функции , снизу графиком функции 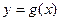 , слева и справа прямыми , слева и справа прямыми  и и 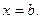
| 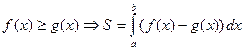
|
Пример.. Вычислить площадь фигуры, ограниченной линиями:
а) 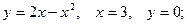 б)
б) 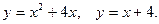
Решение.
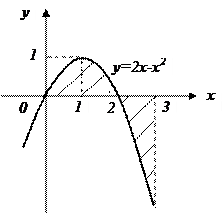 а) Построим фигуру, площадь которой требуется найти (рис. 39).
а) Построим фигуру, площадь которой требуется найти (рис. 39).
Кривая 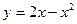 является параболой с вершиной в точке
является параболой с вершиной в точке 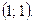 Парабола пересекает ось
Парабола пересекает ось 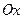 в точках
в точках 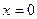 и
и 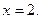 Фигура состоит из двух частей, следовательно
Фигура состоит из двух частей, следовательно 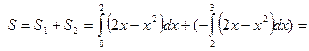
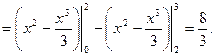
Рис. 39
 б) Для построения фигуры, площадь которой требуется найти, найдем точки пересечения параболы
б) Для построения фигуры, площадь которой требуется найти, найдем точки пересечения параболы 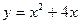 и прямой
и прямой 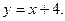 Решим СЛАУ:
Решим СЛАУ:
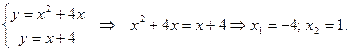
Построим прямую 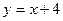 и параболу
и параболу 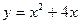 с вершиной
с вершиной 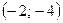 и точками пересечения оси
и точками пересечения оси  в
в 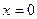 и
и 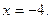 Строим прямую и параболу (рис. 40)
Строим прямую и параболу (рис. 40)
Рис. 40
Имеем, 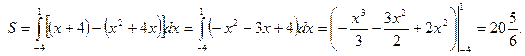
Вычисление длины дуги кривой
Если функция 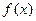 непрерывна вместе с
непрерывна вместе с 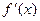 на отрезке
на отрезке 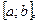 то длина дуги
то длина дуги 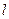 кривой АВ выражается формулой
кривой АВ выражается формулой 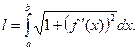
Пример. Найти длину дуги полукубической параболы 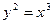 от точки
от точки 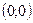 до точки
до точки 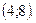
Решение. Полукубическая парабола 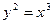 симметрична относительно оси
симметрична относительно оси 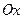 (см. рис….). Точки
(см. рис….). Точки 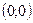 и
и 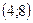 лежат на верхней ветви параболы, которая описывается уравнением
лежат на верхней ветви параболы, которая описывается уравнением 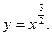 Тогда
Тогда 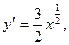 и по формуле имеем:
и по формуле имеем: 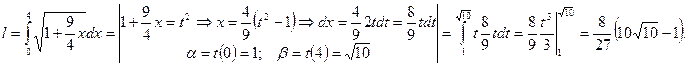
Вычисление объема тела вращения
| № | Рисунок | Формула |
 Тело образовано вращением вокруг оси
Тело образовано вращением вокруг оси 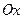 криволинейной трапеции, ограниченной сверху графиком функции криволинейной трапеции, ограниченной сверху графиком функции 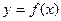 , снизу осью , снизу осью 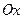 , слева и справа прямыми , слева и справа прямыми  и и 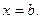
| 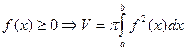
| |
….
Тело образовано вращением вокруг оси 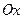 криволинейной трапеции, ограниченной сверху графиком функции криволинейной трапеции, ограниченной сверху графиком функции 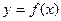 , снизу графиком функции , снизу графиком функции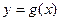 , слева и справа прямыми , слева и справа прямыми  и и 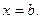
| 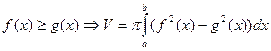
|
Отечественная школа физического воспитания имеет богатый опыт. В то же время не меньшими, а иногда и большими знаниями и методами их реализации обладают зарубежные системы. Поэтому естественный процесс взаимодополнения их расширяет возможности в достижении оздоровительного эффекта, рационализации всей оздоровительной системы.
Однако при этом важно не прямое заимствование зарубежных национальных систем физических упражнений, а их адаптация к отечественному менталитету и исторически сложившейся отечественной системе физического воспитания. Это в наибольшей мере относится к так называемым восточным системам, некоторые из которых уже преодолели национальные границы и, с подачи определенного рекламного обеспечения, представляются как «самые универсальные». Многие их характеристики справедливы. Однако...
Восточные системы физических упражнений впитали в себя многовековые традиции и богатый опыт многих поколений, позволяющий познавать и использовать скрытые резервы человека, развивать его психофизические качества в гармонии с окружающей средой.
Отличительными особенностями восточных оздоровительных систем являются:
1) религиозно-философские основы;
2) ритуальность и образность оформления занятий;
3) попытка глубокого осмысления телодвижений и увязывание их с внутренним отражением - процессами, происходящими в организме во время выполнения упражнений, оценкой соответствующих ощущений;
4) строгая регламентация действий, поз и их соединений, соответствующая канонам той или иной системы;
5) использование приемов психической саморегуляции (концентрация внимания на «точке», мысленное проговаривание действия, образность в адресации конкретному органу или функциональной системе, волевое перераспределение напряжений и расслаблений и др.);
6) наличие свода правил-требований, которые определяют манеру и стиль поведения ученика, его общения с учителем;
7)в целом формирование определенного и своеобразного образа жизни.
Различные системы имеют, между тем, специфические особенности. Некоторые из них целесообразно рассмотреть.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1001; Нарушение авторских прав?; Мы поможем в написании вашей работы!