Вычисление двойных интегралов

Продолжая трактовать двойной интеграл геометрически как объем цилиндрического тела, мы дадим здесь указания относительно его вычисления путем сведения к вычислению определенных интегралов.

Теорема. Если функция f(x,y) непрерывна в замкнутой области s, ограниченной линиями х=а, х=b (a<b), y=j(x), y=g(x) (j(x) и g(x) – непрерывные функции на отрезке [a;b], причем j(x)£g(x) на этом отрезке), то имеет место равенство

, (*)

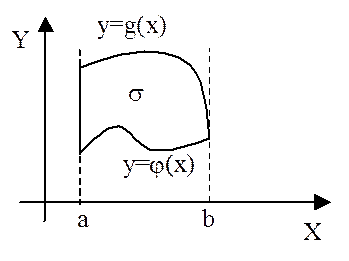
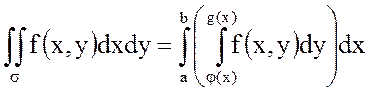позволяющее свести вычисление двойного интеграла к последовательному вычислению определенного интеграла от определенного интеграла (или, что тоже, к вычислению повторного интеграла).

Повторный интеграл, заданный в правой части равенства (*), обычно записывается в виде:

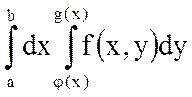
При вычислении двойного интеграла с помощью повторного по формуле (*) сначала вычисляется внутренний интеграл

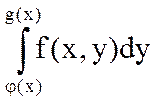
при постоянном значении переменной х в пределах изменения у (для области s), затем полученная функция от х интегрируется по х в максимальных пределах изменения переменной х для области s.

Рассмотрим пример. Вычислить интеграл 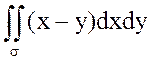, если область s ограничена линиями y=0; y=x³, x=1.

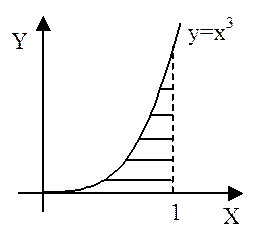
Так как область s и функция f(x,y) удовлетворяют условиям теоремы, получим:

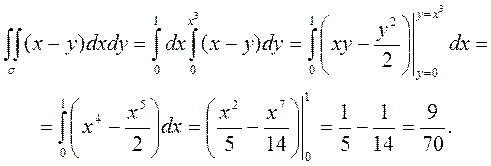
Если область s представляет собой криволинейную трапецию другого типа и ограничена линиями y=c; y=d; (c<d), x=g₁(y); x=g₂(y) (c£y£d), (g₁(y), g₂(y) непрерывные на [c;d] функции, причем всюду на этом отрезке g₁(y)£g₂(y)), то получим формулу

.

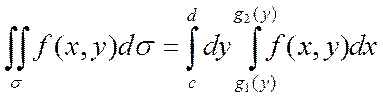Замечание. Если контур области s пересекается лишь в двух точках прямыми, параллельными оси ординат, так и параллельными оси абсцисс (как, например, в случае, изображенном на рис. 2),

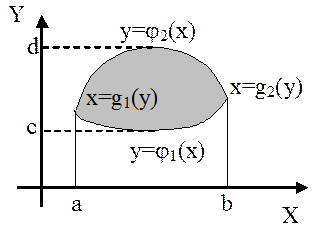
Рис. 2.

то при выполнении указанных условий применимы обе упомянутые формулы. Из сопоставления их получается равенство:

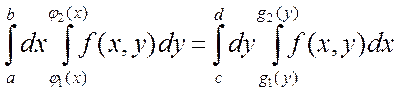
Пример. Вычислить двойной интеграл 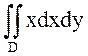по области D, ограниченной линиями y=1-x, y=2, y=x² + 1 (рис. 3).

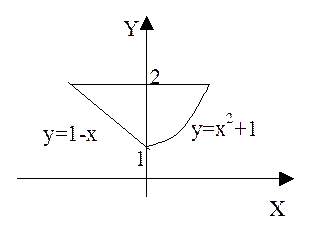
Рис. 3.

Применяя формулу сведения двойного интеграла к повторному (условия теоремы выполнены), получим:

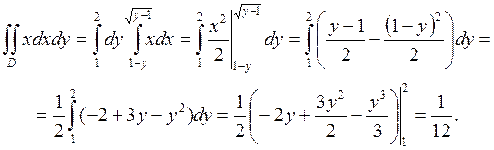
Пример. Найти пределы двукратного интеграла 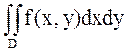для данных (конечных) областях интегрирования D.

1. x²+y²£1, x³0, y³0.

Решение. Полезно сделать чертеж, хотя бы грубо, чтобы получить общее представление об области.

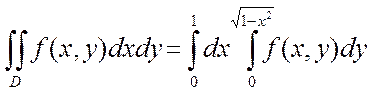, или

.

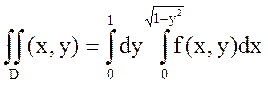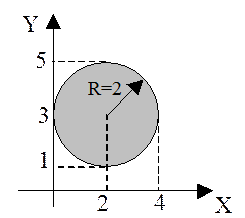
2. (x-2)²+(y-3)² £ 4

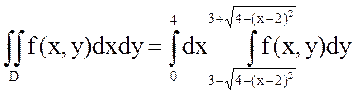, или

.

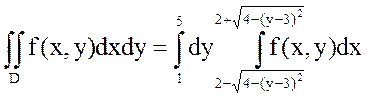Пример. Переменив порядок интегрирования, записать данное выражение в виде одного двукратного интеграла:

1. .

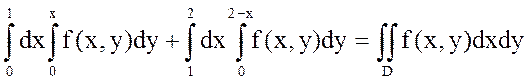Сделаем чертеж области:

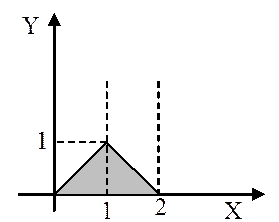
получим .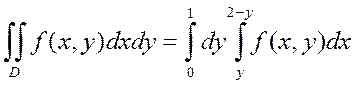

2.

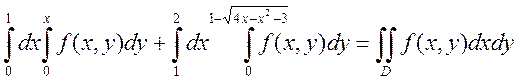
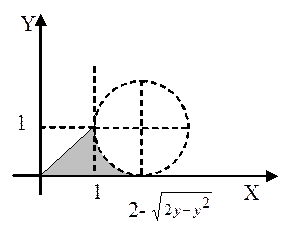
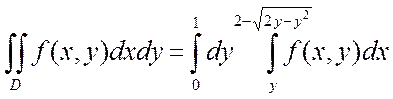
Дата добавления: 2014-01-20