Замена переменных в двойном интеграле. Пусть имеются две плоскости с выбранными на них прямоугольными декартовыми системами координат XOY и UOV

Пусть имеются две плоскости с выбранными на них прямоугольными декартовыми системами координат XOY и UOV. Рассмотрим в этих плоскостях две замкнутые области: область D на плоскости XOY и область s на плоскости UOV, и предположим, что функции:

устанавливают взаимно однозначное соответствие между точками этих областей.

Пусть функции j(U,V) и y(U,V) непрерывны в области s вместе со своими частными производными первого порядка. Тогда определитель

будет непрерывной функцией переменных U и V, определенных в области s. Этот функциональный определитель, называемый определителем Якоби или якобианом отображения (1), принято обозначать J (U,V) или символом 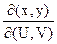. Абсолютная величина Якобиана играет роль коэффициента плоскости UOV при преобразовании ее в плоскость XOY.

Рассмотрим двойной интеграл

от непрерывной функции в заданной области D, ограниченной кусочно-гладкой линией.

Поставим своей целью заменить двойной интеграл по переменным х и у (по области D) равным ему двойным интегралом по переменным U и V (по области s).

Эта цель достигается с помощью формулы замены переменной в двойном интеграле:

.

Применим эту формулу при переходе к полярным координатам: x=r cosa; y=r sina.

Вычислим Якобиан:

О(r,х)===rcos²a+rsin²a=r.

В итоге получим формулу перехода к полярным координатам

Пример. Вычислить интеграл Пуассона 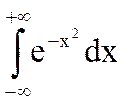. Для вычисления рассмотрим двойной интеграл , где D- четверть круга радиуса R, расположенная в первом квадранте. Преобразуем его к полярным координатам:

.

Предположим, что R®+¥, т.е. область D расширяясь заполняет весь первый квадрант. По аналогии с несобственным интегралом от функции одной переменной запишем

(*)

Примем теперь в качестве области D квадрат 0£x£a; 0£y£a, тогда

.

Т.к. величина определенного интеграла не зависит от обозначения переменной интегрирования, то полученное выражение равно . Устремляя a®¥ получим:

(**).

Сравнивая равенства (*) и (**) получим

или и окончательно .

Дата добавления: 2014-01-20