Структурные характеристики вариационного ряда распределения

Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий

Изучая вариацию по всей совокупности в целом и опираясь на общую среднюю, невозможно определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений признака. Это возможно при помощи аналитической группировки, разделив изучаемую совокупность на однородные группы по признаку-фактору. При этом можно определить три показателя колеблемости признака в совокупности: дисперсию общую, межгрупповую и среднюю из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

Межгрупповая дисперсия () характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:

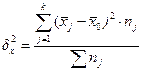
где k - число групп;

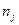- число единиц в j -й группе;

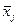- частная средняя по j-й группе;

- общая средняя по совокупности единиц.

Внутригрупповая дисперсия (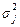) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:

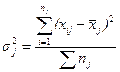
По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий ():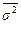

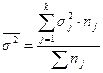
Правило сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

.

Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсий, появляющихся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

Правило сложения дисперсий позволяет выявить зависимость результата от определяющих факторов с помощью соотношения межгрупповой дисперсии и общей дисперсии. Это соотношение называется эмпирическим коэффициентом детерминации ():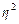

Он показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки.

Корень квадратный из эмпирического коэффициента детерминации носит название эмпирического корреляционного отношения ():

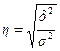
Это отношение характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если , то группировочный признак не оказывает влияния на результативный. Если , то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.

Пример. Рассмотрим правило сложения дисперсий. Имеются данные об объеме выполненных работ проектно-изыскательными организациями на предприятиях разных форм собственности.

Таблица 6

Организация	Объем выполненных работ на предприятиях, млн. руб.
государственных	коммерческих
Итого

1. Определим средний объем выполненных работ на предприятиях двух форм собственности:

2. Определим средние объемы выполненных работ по предприятиям каждой формы собственности:

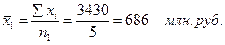
3. Рассчитаем внутригрупповые и общую дисперсии:

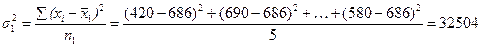
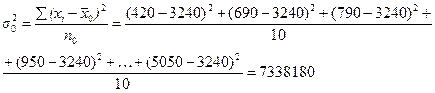
4. Рассчитаем среднюю из внутригрупповых и межгрупповую дисперсии по данным, представленным в табл. 7.

Таблица 7

Расчет 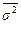и 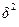по предприятиям двух форм собственности

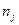
Группы предприятий	Численность предприятий	Средний объем выполненных работ, млн. руб.	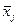Дисперсия объема выполненных работ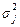
Государственные предприятия Коммерческие предприятия

Средняяиз внутригрупповых дисперсий:

Межгрупповая дисперсия:

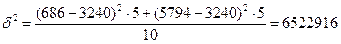
5. Найдем общую дисперсию по правилу сложения дисперсий:

Сопоставив межгрупповую дисперсию с общей дисперсией, рассчитаем коэффициент детерминации:

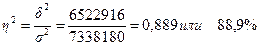
Коэффициент детерминации показывает, что дисперсия объема выполненных работ зависит от формы собственности предприятия на 88,9%. Остальные 11,1% определяются множеством других неучтенных факторов.

Определим эмпирическое корреляционное отношение:

.

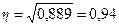Полученное значение эмпирического корреляционного отношения позволяет утверждать, что существует тесная связь между формой собственности предприятия и объемом выполненных проектно-изыскательных работ.

Правило сложения дисперсий для доли признака. Рассмотренное правило сложения дисперсий распространяется и на дисперсии доли признака, т.е. доли единиц с определенным признаком в совокупности, разбитой на группы. При этом изучение вариации происходит непосредственно при вычислении и анализе видов дисперсий для доли признака.

Внутригрупповая дисперсия доли определяется по формуле:

,

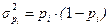где - доля изучаемого признака в отдельных группах.

Средняя из внутригрупповых дисперсий имеет вид:

Межгрупповая дисперсия:

,

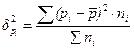где - численность единиц в отдельных группах;

- доля изучаемого признака во всей совокупности.

Доля признака в совокупности определяется по формуле средней арифметической взвешенной:

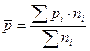
Общая дисперсия определяется по формуле:

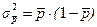
Три вида рассмотренных дисперсий связаны между собой следующим образом: .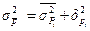

Это соотношение дисперсий называется правилом сложения дисперсий доли признака.

Пример. Имеются следующие данные удельного веса основных рабочих в трех цехах фирмы.

Таблица 8

Удельный вес основных рабочих фирмы

Цех	Удельный вес основных рабочих, %,	Численность всех рабочих, чел.,
Итого	-

1. Определим долю основных рабочих в целом по фирме:

2. Общая дисперсия доли основных рабочих по всей фирме в целом:

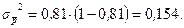
3. Внутрицеховые дисперсии:

4. Средняя из внутригрупповых дисперсий:

5. Межгрупповую дисперсию определим по формуле:

Проверка вычислений показывает: .

В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место (каждое четвертое, пятое, десятое, двадцать пятое и т.д.) в ранжированном вариационном ряду. Такие показатели носят общее название квантилей, или градиентов.

Некоторые квантили имеют особые наименования: квартили, квинтили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квар­тиль нижний , отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний , отсекающий 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине ; 25% единиц будут заключены между и ; 25% - между и и остальные 25% превзойдут . Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.

Для расчета квартилей по интервальному вариационному ряду используются формулы:

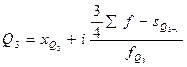
где 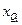- нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);

- нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);

- величина интервала;

- накопленная частота интервала, предшествующего интервалу, содер­жащему нижний квартиль;

- то же для верхнего квартиля;

- частота интервала, содержащего нижний квартиль;

- то же для верхнего квартиля.

Пример. Рассмотрим расчет нижнего и верхнего квартилей по данным, характеризующим коммерческие банки по срокам функционирования (табл. 2). Определим номер для 1-го и 3-го квартилей:

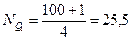
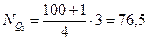
Применяя способ расчета, аналогичный медиане по ряду накопленных частот, определим:

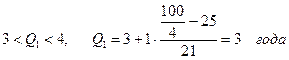
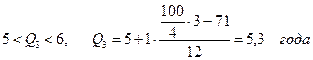
Итак, 25% банков имеют срок функционирования менее 3 лет, 25% банков - свыше 3 лет, а остальные имеют срок функционирования в пределах от 3 до 5,3 года.

Квинтили делят распределение на пять равных частей.

Децили - это значения вариант, которые делят ранжированный ряд на 10 равных частей: 1-й дециль делит совокупность в соотношении 1/10 к 9/10, 2-й дециль - в соотношении 2/10 к 8/10 и т.д.

Вычисляются децили по той же схеме, что и медиана, и квартили:

, ,……..,

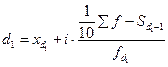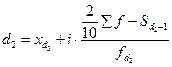Пример. По табл. 2 рассчитать 1-й и 9-й децили.

Определим номер для 1-го и 9-го децилей:

По ряду накопленных частот определим:

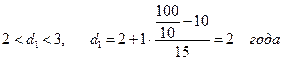
Это означает, что 10% коммерческих банков имеют срок функционирования менее 2 лет, а 90% банков имеют срок функционирования свыше 2 лет.

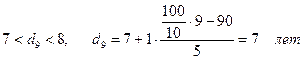
90% банков имеют срок функционирования меньше 7 лет, а 10% банков имеют срок функционирования свыше 7 лет.

Дата добавления: 2014-01-20