Изучение формы распределения

Для обобщающей характеристики особенностей формы распределения применяются кривые распределения. Кривая распределения выражает графически (полигон, гистограмма) закономерность распределения единиц совокупности по величине варьирующего признака. Различают эмпирические и теоретические кривые распределения.

Эмпирическая кривая распределения - это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.

Теоретическая кривая распределения - это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений.

Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута - правая или левая, различают правостороннюю или левостороннюю асимметрию. Кривые распределения могут быть одно-, двух- и многовершинными.

Для однородных совокупностей характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп. Для симметричных распределений частоты любых двух вариант, равноотстоящих в обе стороны от центра, равны между собой. Рассчитанные для таких рядов распределений характеристики равны: , , . Если указанные соотношения нарушены, то это свидетельствует о наличии асимметрии распределения. 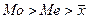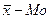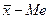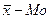При разности между иположительные и асимметрия правосторонняя, а при , наоборот, разности и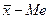отрицательные и асимметрия левосторонняя.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии :

или

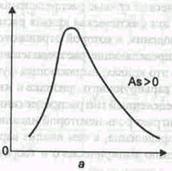Правосторонняя асимметрия

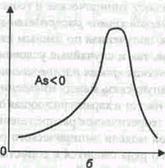Левосторонняя асимметрия

В симметричном распределении центральный момент 3-го порядка 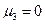, поэтому, чем он больше, тем больше и асимметрия. Эта особенность и используется для характеристики асимметрии. Коэффициент асимметрии равен отношению центрального момента 3-го порядка к среднему квадратическому отклонению в кубе, т.е.

Чем числитель ближе к 0, тем асимметрия меньше. Этот показатель асимметрии более точен по сравнению с предыдущими и применяется более широко. Асимметрия выше 0,5 (независимо от знака) считается значительной; если она меньше 0,25, то незначительной.

Оценка существенности проводится на основе средней квадратической ошибки коэффициента асимметрии , которая зависит от числа наблюдений п и рассчитывается по формуле:

В случае асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами.

Пример. Вычислить коэффициент асимметрии.

Распределение коммерческих банков по размеру выданных кредитов

Группы банков по размеру кредита, млн. руб. х	Число банков f	Середина интервала
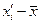
1-6		3,5		-10		-6000
6-11		8,5	25,5	-5		-375
11-16		13,5	148,5
16-21		18,5	92,5
21-26		23,5	117,5
Итого		-		-		-750

На основе полученных данных определим коэффициент асимметрии, для этого определим центральный момент второго и третьего порядков.

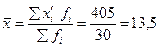
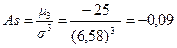
Полученный результат свидетельствует о наличии незначительной по величине и отрицательной по своему характеру асимметрии.

Для симметричных распределений может быть рассчитан показатель эксцесса . Наиболее точно он определяется по формуле с использованием центрального момента 4-го порядка ( ):

Среднеквадратическая ошибка эксцесса 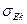рассчитывается поформуле:

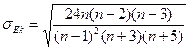, где n - число наблюдений.

Островершинное распределение

Плосковершинное распределение

В нормальном распределении .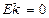

Так как показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определенные указания для дальнейшего исследования социально-экономических явлений. Например, появление значительного отрицательного эксцесса может указывать на качественную неоднородность исследуемой совокупности. Эти показатели позволяют сделать вывод о возможности отнесения данного эмпирического распределения к типу кривых нормального распределения.

Дата добавления: 2014-01-20