Использование эталона длины для определения площади и объема физических тел. Уравнения связи

Производная физическая величина – площадь

Площади плоских поверхностей, имеющих форму прямоугольников, определяются путём перемножения двух сторон.

Площадь пола помещения, например, определяется путём перемножения длины пола на его ширину:

.

В обозначениях:

.

Площадь прямоугольного треугольника равна половине произведения катетов:

.

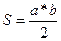Площадь поверхности цилиндра определяется по формуле:

,

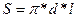где π = 3,14; d – диаметр цилиндра; l – длина цилиндра.

Площадь круга равна:

,

где d – диаметр круга.

Площадь поверхности шара: ,

где d – диаметр шара.

Единицей измерения площади является кваметр; обозначение – квм. Один кваметр равен площади квадрата со стороной в один метр размерный: 1 квм = 1 мр * 1 мр.

Размерность площади: квм = мр².

Взаимные зависимости:

прямоугольника: ; ;

прямоугольного треугольника: ; ;

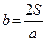цилиндра: ; ;

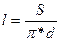круга: ;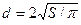

шара: .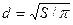

Производная физическая величина – объём размерный

Одним из примеров объёма размерного является объём параллепипеда; он определяется путём перемножения трёх его размеров: длины, ширины и высоты.

Объём размерный принято обозначать большой латинской буквой V.

Объём помещения = длина * ширина * высота.

В обозначениях:

.

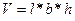Объём цилиндра определяется по формуле:

,

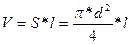где S – площадь торца цилиндра; l – длина цилиндра; d – диаметр цилиндра.

Объём шара:

.

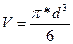Единицей измерения объёма размерного является кубометр; обозначение – кбм.

Один кубометр равен объёму куба со стороной в один метр размерный: 1кбм = 1мр *1мр * 1 мр.

Размерность объёма размерного: кбм = мр³.

Взаимные зависимости:

помещения:

; ; ;

цилиндра:

;

;

шара:

.

Площадь прямоугольника Площадь круга Объем параллелепипеда Объем цилиндра Длину окружности

S = lb S = пR^2V = Sh V – Sh L – 2пR

Площадь — квадратный метр (м², кв.м, m², sq.m); квадратный миллиметр (мм², кв.мм) = 10^–6 м²
квадратный сантиметр (см², кв.см) = 10^–4 м²
сотка = 100 м²
ар = 100 м²
гектар (га) = 100 соток = 100 ар = 10⁴м²
квадратный километр (км², кв.км) = 100 га = 10⁶ м^2;;

квадратный дюйм (square inch, sq.in.) = 6.45 см² = 6.45·10^–4 м²
квадратный фут (square foot, sq.ft.) = 929.03 см² = 9.2903·10^–2 м²
квадратный ярд (square yard, sq.yd.) = 0.836126 м²
акр (acre, a.) = 400 м²
квадратная миля (square mile, sq.mi.) = 2.59 км² = 2.59·10⁶ м²

Объём, ёмкость — кубический метр (м³, куб.м, m³, cu.m)

кубический миллиметр (мм³, куб.мм) = 10^–9 м³
кубический сантиметр (см³, куб.см), миллилитр (мл, ml) = 10^–6 м³
литр (л, l)= 1 дм³ = 1000 см³ = 10^–3 м³
кубический километр (км³, куб.км) = 10⁹ м³

кубический дюйм (cubic inch, cu.in.) = 16.387 см³ = 1.6387·10^–5 м²
кубический фут (cubic foot, cu.ft.) = 28.317 л = 2.8137·10^–2 м³
кубический ярд (cubic yard, cu.yd.) = 0.765 м³
регистровая тонна (register ton, reg.ton) = 2.832 м³
пинта (pint, pt.) = 0.142 л = 1.42·10^–4 м³
пинта США для сыпучих веществ (US dry pint) = 0.551 л = 5.51·10^–4 м³
пинта США для жидкостей (US liquid pint) = 0.473 л = 4.73·10^–4 м³
кварта (quart, qt.) = 1.136 л = 1.136·10^–3 м³
кварта США для сыпучих веществ (US dry quart) = 1.1 л = 1.1·10^–3 м³
кварта США для жидкостей (US liquid quart) = 0.946 л = 9.46·10^–4 м³
галлон стандартный (gallon, gal.) = 4.546 л = 4.546·10^–3 м³
галлон США для сыпучих веществ (US dry gallon) = 4.4 л = 4.4·10^–3 м³
галлон США для жидкостей (US liquid gallon) = 3.785 л = 3.785·10^–3 м³
бушель стандартный (bushel, bu.,bus) = 36.35 л = 3.635·10^–2 м³
баррель стандартный (barrel, bbl., bl.) = 163.6 л = 0.1636 м³
баррель США (US barrel) = 119 л = 0.119 м³
нефтяной баррель (US barrel petroleum) = 158.97 л = 0.15897 м³
четверть стандартная (quarter, qr.) = 290.8 л = 0.2908 м³
русское ведро = 12.30 л = 1.230·10^–2 м³

Примеры:

5 км² = 5(10³ м)² = 5×10⁶ м²;

250 см³/с = 250(10^{-2 м)3}/(1с) = 250×10^-6 м³/с;

0,002 см^-1 = 0,002(10^{-2 м)-1} = 0,002×100 м^-1 = 0,2 м^-1.

1. Числа округляются до определенного разряда путем отбрасывания значащих цифр справа с возможным изменением цифры этого разряда.

Например, округление числа 132,482 до четырех значащих цифр дает 132,5.

В случае если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется.

Например, округление числа 12,23 до трех значащих цифр дает 12,2.

В случае если первая из отбрасываемых цифр (считая слева направо) равна или более 5, то последняя сохраняемая цифра увеличивается на единицу.

Например, округление числа 0,145 или 0,147 до двух значащих цифр дает 0,15.

2. Числа следует округлять сразу до желаемого количества значащих цифр, а не по этапам.

Например, число 565,46 округляется до трех значащих цифр - до 565. Округление по этапам привело бы к 565,5 на I этапе и 566 (ошибочно) на II этапе.

Примечание. В тех случаях, когда следует учитывать результаты предыдущих округлений, необходимо поступать следующим образом:

а) если отбрасываемая цифра получилась в результате предыдущего округления в большую сторону, то последняя оставшаяся цифра сохраняется;

б) если отбрасываемая цифра получилась в результате предыдущего округления в меньшую сторону, то последняя оставшаяся цифра увеличивается на единицу (с переходом при необходимости в следующие разряды).

Например, округление до одной значащей цифры числа 0,15, полученного после округления:

числа 0,149 дает 0,1;

числа 0,153 дает 0,2.

3. Целые числа округляются, следующим образом:

Например, округление числа 12456 до двух значащих цифр дает 12×10³.

Метр квадратный	m²	Площадь квадрата, сторона которого равна 1 метру
Метр кубический	m³	Объем куба с длиной ребра, равной 1 метру

Обьём

m³, cm³, L³

количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объём тесно связано понятие вместимость. Под вместимостью понимают объём внутреннего пространства сосуда или аппарата, укладочных ящиков и т. д

Площадь

S

Одна из количественных характеристик плоских геометрических фигур и поверхностей

Дата добавления: 2014-01-20