Внутренние силы и напряжения. Закон Гука и принцип независимости действия сил

Закон Гука и принцип независимости действия сил

Многочисленные экспериментальные наблюдения за поведени­ем деформируемых тел показывают, что в определенных диапазо­нах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Гуком и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взя­той точки А нагруженного тела по некоторому направ­лению, например, по оси x, а может быть выражено следующим образом:

u = d _x P, (3.1)

где Р - сила, под действием которой происходит перемещение u; d _{x ×}- коэффициент пропорциональности между силой и перемеще­нием.

Очевидно, что коэффициент d _x зависит от физико-механиче­ских свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей си­стемы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную за­висимость между напряжениями и деформациями, а не между си­лой и перемещением. Коэффициенты пропорциональности в этом случае представляют собой физико-механические характеристики материала и уже не связаны с геометрическими особенностями си­стемы в целом.

Системы, для которых соблюдается условие пропорционально­сти между перемещениями и внешними силами, подчиняются принципу суперпозиции, или принципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе прило­жено несколько сил, то можно определить внутренние силы, на­пряжения, перемещения и деформации от каждой силы в отдель­ности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.

Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого прило­жены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 3.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня.

Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 3.1, б), приходим к следующему уравнению:

P + N_z = 0,

откуда следует, что

N_z = P = const.

Примем для N_z следующее правило знаков. Если N_z направлена от сечения, т.е. вызывает положительную деформацию (растяже­ние), то она считается положительной. В обратном случае - отри­цательной.

Рис. 3.1

Нормальная сила N_z приложена в центре тяжести сечения, яв­ляется равнодействующей внутренних сил в сечении и, в соответст­вии с этим, определяется следующим образом:

.

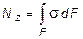Но из этой формулы нельзя найти закон распределения нор­мальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямо­угольную сетку (рис. 3.1, б), то после нагружения поперечные ли­нии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что по­перечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации.

Значит, все продольные волокна стержня находятся в одина­ковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и рав­ны

,

где F - площадь поперечного сечения стержня.

Высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения пло­щади поперечного сечения (рис. 3.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций. Основанием для такого утверждения служит принцип Сен - Венана, справедливый для любого типа напря­женного состояния и формулируемый следующим образом: осо­бенности приложения внешних нагрузок проявля­ются, как правило, на расстояниях, не превыша­ющих характерных размеров поперечного сечения стержня.

Дата добавления: 2014-01-20