Напряженное и деформированное состояние при растяжении и сжатии

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол a с плоскостью нормального сечения (рис. 3.6, а).

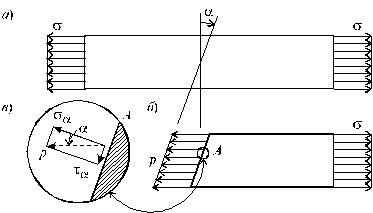
Рис. 3.6

Из условия å z = 0, записанного для отсеченной части стержня (рис. 3.6, б), получим:

р F _a = s F, (3.8)

где F - площадь поперечного сечения стержня, F _a = F /cos a - пло­щадь наклонного сечения. Из (3.8) легко установить:

р = s сos a. (3.9)

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 3.6, в), с учетом (3.9) получим:

s_a = p cos a = s cos² a; t_a = p sin a = s sin 2 a. (3.10)

Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла a. При a = 0 из (3.10) следует, что s_a = s, t_a = 0. При a = , т.е. на продольных площадках, s_a = t_a = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения t_a принимают наибольшие зна­чения при a = 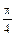, и их величина составляет t_max=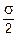. Важно отме­тить, как это следует из (3.10), что 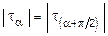. Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит назва­ние закона парности касательных напряжений.

Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направ­лении сопровождается пропорциональным уменьшением попереч­ных размеров стержня (рис. 3.7).

Рис. 3.7

Если обозначить:

e_прод = ; e_попер = -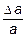, m = -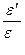, (3.11)

то, как показывают эксперименты, m = const для данного материала и является безразмерным коэффициентом Пуассона. Вели­чина m является важной характеристикой материала и определяется экспериментально. Для реальных материалов m принимает значе­ния 0,1 ¸ 0,45.

При растяжении стержня возникают не только линейные, но и угловые деформации.

Рассмотрим прямой угол АВС (рис. 3.8, а), образованный отрез­ками АВ и АС, в недеформированном состоянии.

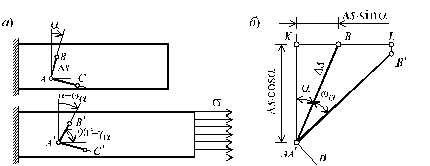
Рис. 3.8

При растяжении стержня точки А, В и С займут положение А ¢, B ¢, C ¢ соответственно. Величина

g_a = Ð ВАС - Ð А ¢ B ¢ C ¢

называется угловой деформацией или угловым сдвигом в точке А.

Совместим точки А и А ¢ и рассмотрим взаимное расположение отрезков АВ и А ¢ B ¢(рис. 3.8, б). На этом рисунке отметим вспомо­гательные точки K и L и прямую n, перпендикулярную отрезку А ¢ B ¢. Из рис. 3.8, б имеем:

e_прод = 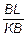; e_попер = ,

откуда с учетом e_прод = получим:

. (3.12)

Для определения w_a спроектируем ломаную ВLB ¢ А ¢на ось n D S ×sin w_a = BL cos (a + w_a) + LB ¢sin(a + w_a), откуда, учитывая ма­лость угла w_a, т.е. sin w_a» w_a, cos w_a» 1, получим:

w_a = 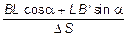. (3.13)

В результате совместного рассмотрения (3.12) и (3.13) получим:

w_a = .

Откуда

.

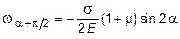Следовательно,

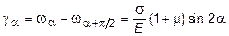. (3.14)

Сопоставляя выражение g_a с выражением t_a из (2.17) окон­чательно получим закон Гука для сдвига:

(3.15)

где величина называется модулем сдвига или модулем упругости материала второго рода.

Дата добавления: 2014-01-20