Матрица смежности

Представление графа в ЭВМ.

Пусть дан смешанный граф:

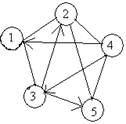Рис. 6. Смешанный граф.

Известно несколько способов представлений графа G=(V, Е) в памяти компьютера.

Матрица смежности - это матрица размером n×n, в которой c_ij =1, если существует ребро из i в j и c_ij =0 в противном случае.

Например, составим для вышеприведенного графа матрицу смежности:

Для неориентированного графа справедливо c_ij = c_ji и матрица называется симметрической.

Представление в виде матрицы смежностей удобно для тех алгоритмов на графах, которым часто нужно знать, есть ли в графе данное ребро, ибо время, необходимое для определения наличия ребра, фиксировано.
Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос "существует ли ребро из v в w?".

Недостаток этого способа заключается в том, что способ пригоден только для простых графов.

Дата добавления: 2014-01-20