
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Списки смежности
|
|
|
|
Списки инцидентности.
Массив ребер.
Массив ребер – это массив, в котором ребра хранятся парами вершин, которые они соединяют.
Это наиболее понятный, но достаточно неудобный способ хранения графа. Однако у него есть один большой плюс - при таком способе представления легко вводить дополнительные характеристики ребер. Например, чтобы сохранить веса ребер, достаточно сделать массив размером Mx3 и в дополнительную ячейку для каждого ребра записать его вес.
Например, для графа, приведенного на рис.6 массив ребер будет следующий: (1,2), (1,3), (2,1), (2,4), (2,5), (3,1), (3,2), (3,5), (4,1), (4,2), (4,3), (4,5), (5,2), (5,4).
Если априорно известно, что граф не ориентированный, то включая описание (v, w) не включается описание (w, v).
Для каждой вершины графа создаются три списка:
ü v 0: только неориентированные ребра, инцидентные вершине;
ü v +: исходящие ребра;
ü v -: входящие ребра.
Ели граф ориентирован, то для каждой вершины v достаточно списков v + и v -. Если граф неориентированный, то достаточно списков v 0.
Например,
| 10: | (1,2),(1,3) |
| 1+: | |
| 1-: | |
| 20: | (2,1), (2,4), (2,5) |
| 2+: | |
| 2-: | (3,2) |
| 30: | (3,1) |
| 3+: | (3,2), (3,5) |
| 3-: | (4,3) |
| 40: | (4,2), (4,5) |
| 4+: | (4,1), (4,3) |
| 4-: | |
| 50: | (5,4), (5,2) |
| 5+: | |
| 5-: | (3,5) |
Представляет собой структуру данных, которая для каждой вершины графа хранит список смежных с ней вершин. Список представляет собой массив указателей, i-ый элемент которого содержит указатель на список вершин, смежных с i-ой вершиной.
Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.
Например (рис.6):
| 1: | 2,3 |
| 2: | 1,4,5 |
| 3: | 1,2,5 |
| 4: | 1,2,3,5 |
| 5: | 1,4 |
Матрицей инцидентности (инциденций) неориентированного графа называется матрица 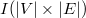 , для которой , для которой  , если вершина , если вершина  инцидентна ребру инцидентна ребру 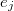 , в противном случае , в противном случае  . .
|
Матрицей инцидентности (инциденций) ориентированного графа называется матрица 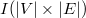 , для которой , для которой  , если вершина , если вершина  является началом дуги является началом дуги 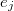 , , 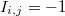 , если , если  является концом дуги является концом дуги 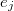 , в остальных случаях , в остальных случаях 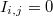 . .
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1156; Нарушение авторских прав?; Мы поможем в написании вашей работы!