Математическая модель

Системы с одной степенью свободы

Податливость определяется аналитически или численно. Ее определение не представляет проблемы да же в сложных конструкциях. Так как есть множество расчетных пакетов для статики. Мера инерции – масса или момент инерции массы также легко определяется расчетом или экспериментально (см. теоретическую механику). Для многих типовых конструкций перемещения (т.е. податливости) приводятся в справочниках.

Рассмотрим еще один характерный пример – вал с массивным диском массой m и моментом инерции массы J_m по средине. Массой вала пренебрегаем.

R

Система имеет две независимые степени свободы – вертикальное перемещение и поворот в плоскости. Их независимость определяется тем, что ввиду симметрии задачи поворот не вызывает перемещения и наоборот. В первом случае мера инерции m, а податливость 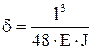. Во втором случае

мера инерции , а податливость . Значения податливостей легко определяются аналитически. Оставим это упражнение по расчету поперечного изгиба на подготовку к экзамену.

Заметим, что малейшая несимметрия в этой задаче приводит в системе с двумя степенями свободы.

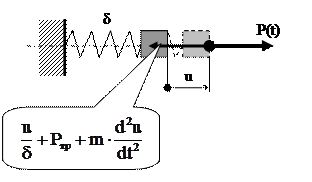В дальнейшем изложении для сокращения записей меру инерции будем обозначать m, а внешние нагрузки считать силами. Среди действующих сил выделим кроме внешних воздействий P(t) (силовое возбуждение) внутренние: от упругого элемента (u/δ), силы трения (Р_тр ) (сопротивления движению), силу инерции 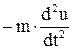и сформулируем условие равновесия инерционного элемента .

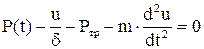После преобразования

. (*)

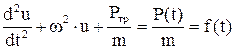
В формуле обозначено .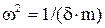
Модель замыкается начальными условиями: .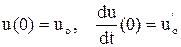

Вид уравнения (*) и его решения существенно зависят от Р_тр.

Сила трения в общем случае определяется свойствами среды и параметрами движения. При незначительном трении, величиной которого можно пренебречь, и при трении, пропорциональном скорости, уравнение (*) линейно и имеет аналитическое решение. Во всех остальных случаях (сухое трение, трение, зависящее от степени скорости и ускорения, и др.) возможно только численное решение. Решение всегда приближенно, так как модель не полностью соответствует объекту. Важно правильно оценивать степень приближенности при не учете некоторых факторов, что будет сделано ниже.

Дата добавления: 2014-01-20