Решение без учета трения

Основное уравнение принимает вид

, (**)

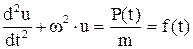линейно; решение состоит из общего решения однородного уравнения 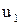и частного решения уравнения с правой частью 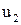, т.е.

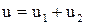
При этом, решая методом Эйлера, получаем

,

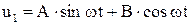а частное решение ищем в виде правой части или методом вариации произвольных постоянных.

Рассмотрим основные задачи динамики для этого случая.

1.Очевидно, что 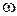- круговая частота собственных колебаний и равна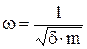

и мы решили первую основную задачу.

2. Динамический коэффициент при ударе получим в двух вариантах.

Первый – удар с известной скоростью V при P(t)=0. В этом случае u₂ =0, начальные условия: u(0)=0, , откуда B=0, и

.

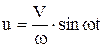Сила удара 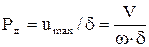, а коэффициент динамичности

.

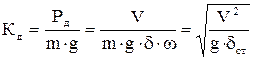Здесь обозначено 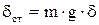- статическое перемещение, т.е. перемещение от статического приложения веса ударяющего груза.

Второй – удар груза, падающего с высоты H. При этом скорость при ударе , , 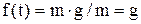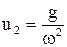и решение

.

С учетом граничных услови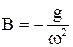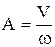й , и

.

Откуда ,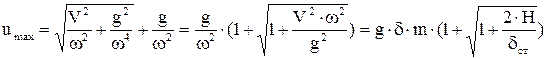

.

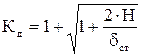Решена вторая основная задача.

3. Исследуем АЧХ при периодическом возмущении от вибрации основания (кинематическое возбуждение). Уравнение равновесия

приводит к дифференциальному уравнению

.

Частное решение в виде правой части

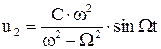
определяет вынужденные колебания. Коэффициент динамичности – отношение амплитуды вынужденных колебаний основания

, а его зависимость от отношения 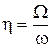и есть АЧХ. Защита от вибраций наступает при 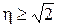когда [К_д ] ≤ 1. До этого вибрации больше возбуждения и возможен резонанс.

Резонанс наступает не мгновенно. Рассмотрим процесс подробнее.

.

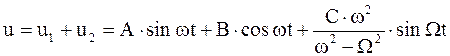При нулевых начальных условиях 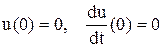после преобразований

.

При получаем неопределенность типа 0/0. Раскрывая по правилу Лопиталя, имеем

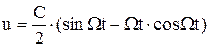
Период вынужденных колебаний

,

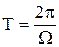и окончательно получаем при резонансе

.

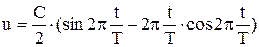График развития резонанса представлен на рисунке. Если резонанс длится не более Т/2, то К_д<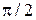, при 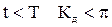и т.д. Таким образом, виброзащита в одномассовой системе достигается при 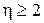и быстром разгоне до таких частот при запуске.

Решена третья задача динамики.

Дата добавления: 2014-01-20