Математическая модель. Системы с несколькими степенями свободы

Системы с несколькими степенями свободы

(на примере двухмассовой)

Податливости δ₁₁, δ₁₂ = δ₂₁, δ₂₂ определяется аналитически или численно. Их определение не представляет проблемы даже в сложных конструкциях. Однако при численном определении податливостей погрешности вычисления могут существенно влиять на точность определение собственных круговых частот. Поэтому при интегрировании дифференциальных уравнений необходимо повышать настройку точности поиска решения, уменьшать шаг интегрирования или переходить от метода Эйлера к методам Рунге-Кутта.

Математическая модель n-массовой системы строится аналогично двухмассовой. Поэтому мы ограничимся подробным рассмотрением только двухмассовой модели. Как и выше, для сокращения записей будем считать мерой инерции массы, а внешними воздействиями силы. Сразу учтем возможное кинематическое возбуждение.

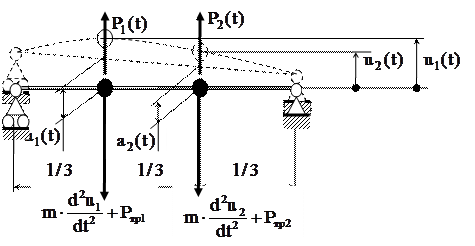
Решение иллюстрируем на следующем тестовом примере.

Аналитическое решение для податливостей в примере (приводится без вывода, вывод на самостоятельную проработку к экзамену)

.

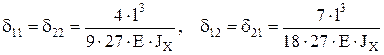Вычисляя перемещения в каждом направлении (степени свободы) получаем для двухмассовой системы

,

, (*)

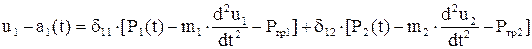систему дифференциальных уравнений, которая совместно с начальными условиями: 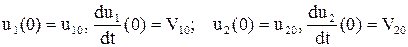составляет разрешающую систему уравнений. Нетрудно продлить модель на n-массовую систему.

Рассмотрим основные задачи динамики, принимая во внимание результаты анализа одномассовой модели.

Дата добавления: 2014-01-20