Частоты собственных поперечных колебаний однородного стержня

Система (13.2) после последовательного дифференцирования по z и подстановок дает

.

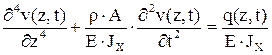Уравнение линейно. Рассмотрим только собственные колебания.

Представим решение в виде 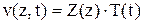и подставим в однородное уравнение. Получаем

,

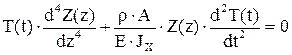и, после преобразования (разделения переменных),

.

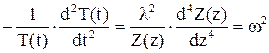Введено обозначение 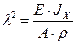. Система распадается на два обыкновенных дифференциальных уравнения

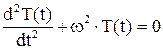и ,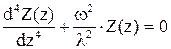

решение которых: ,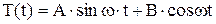

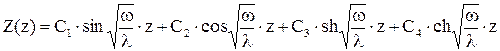
должно удовлетворять граничным и начальным условиям задачи.

Определим частоты собственных колебаний стержня. Для этого достаточно удовлетворить граничным условиям, приравнять нулю определитель полученной системы линейных уравнений относительно С₁… С₄, и, решив полученное трансцендентное уравнение аналитически или численно, определить 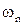. Например, для шарнирно опертого однородного стержня получаем

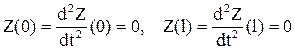, и

.

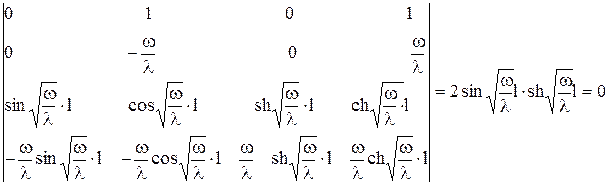Откуда .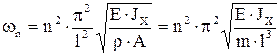

Дата добавления: 2014-01-20