Планы скоростей и ускорений шарнирного четырёхзвенника

Графоаналитический метод кинематического анализа

Лекция 4-2011

Графоаналитический метод называют методом планов скоростей и ускорений.

Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.

Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.

Преимущество этого метода по сравнению с графическим в том, что он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.

Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и его звеньев).

При решении задач такого типа известны угловая скорость w₁ ведущего звена 1 – кривошипа, длины звеньев и координаты неподвижных точек.

Последовательность решения задачи:

1. Строится план механизма (рис. 2.2) в выбранном масштабе длин:

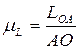, м/мм,

где L_OA – длина кривошипа, м; AO – длина отрезка, изображающего кривошип на плане механизма, мм.

Для построения плана механизма остальные длины звеньев и координаты неподвижных точек шарнирного четырехзвенника (рис. 2.2) переводятся масштабом длин m_L в отрезки:

AB = L_AB/m_L, мм,

BC = L_BC/m_L, мм,

OC = L_OC/m_L, мм.

2. Составляются векторные уравнения линейных скоростей отдельных точек, принадлежащих звеньям механизма.

Векторное уравнение для звена 2 (шатуна)

V _В = V _А + V _ВА, (4.1)

где V _А = V _АО – скорость точки А, которая равна скорости точки А относительно оси вращения кривошипа точки О; V _ВА – вектор относительной скорости точки В шатуна относительно А имеет направление, перпендикулярное отрезку АВ на плане механизма.

Векторное уравнение для звена 3 (коромысла)

V _В = V _С + V _ВС. (4.2)

Так как точка С (ось вращения коромысла 3) неподвижна, то её скорость равна нулю (V _С = 0), а вектор относительной скорости точки В относительно С (V _ВС) имеет направление, перпендикулярное отрезку ВС на плане механизма.

3. Строится план скоростей механизма – это не что иное, как графическое изображение на чертеже векторных уравнений (4.1) и (4.2) в каком-либо масштабе.

План скоростей механизма и его свойства

План скоростей желательно строить рядом с планом механизма Предварительно рассчитывается скорость точки А кривошипа:

, м/с.

Затем выбирается масштаб плана скоростей m_u по соотношению

, ,

где u_A – скорость точки А, м/с; P_Va – длина отрезка, изображающего на будущем плане скоростей скорость V _A, выбирается произвольной длины в мм; при выборе желательно придерживаться условий: во-первых, план скоростей должен размещаться на отведённом месте чертежа, во-вторых, численное значение масштаба m_u должно быть удобным для расчётов (m_u должно быть круглым числом).

После этого можно приступать к построению плана скоростей механизма. Его следует проводить в последовательности, соответствующей написанию векторных уравнений (4.1) и (4.2).

Сначала проводится из произвольно выбранной рядом с планом механизма точки Р_u (полюса плана скоростей) вектор скорости V _А, который перпендикулярен отрезку ОА на плане механизма и имеет длину P_Va, выбранную нами при определении масштаба плана скоростей m_u. Затем через точку a проводится линия, перпендикулярная отрезку АВ плана механизма, а через полюс P_V – линия, перпендикулярная отрезку ВС. Пересечение этих линий даёт точку b. В соответствии с векторными уравнениями (4.1) и (4.2) на построенном плане наносятся направления (стрелки) векторов V _В и V _ВА.

Рис. 2.2. 2 кл. 1 вид. Построение планов скоростей и ускорений.

Определим скорость точки К, принадлежащей шатуну. Для неё можно записать векторные уравнения скоростей:

V _К = V _А + V _КА,

V _К = V _В + V _КВ,

где вектор скорости V _КА перпендикулярен отрезку АК на плане механизма, а вектор V _КВ – отрезку КВ.

При этом из точки a плана скоростей проводим линию, перпендикулярную отрезку АК, а через точку b плана скоростей – линию, перпендикулярную отрезку ВК плана механизма. Построением этих векторных уравнений получаем точку k на плане скоростей. Величину скорости точки К можно вычислить по формуле

V_К = (Р_Vk)m_V,

где Р_Vk – длина соответствующего вектора на плане скоростей.

Можно заметить, что треугольники на плане скоростей и плане механизма подобны:

,

так как стороны их взаимно перпендикулярны. Это свойство можно использовать для определения скорости любой другой точки, принадлежащей какому-либо звену механизма. Отсюда следует теорема подобия: отрезки относительных скоростей на плане скоростей образуют фигуру, подобную фигуре соответствующего звена на плане механизма. Стороны фигур взаимно перпендикулярны.

Угловые скорости шатуна 2 и коромысла 3 рассчитываются по формулам

, c^-1,

, c^-1.

Направления угловых скоростей определяются по направлениям векторов V _ВА и V _BC. Для этого вектор V _ВА условно переносится в точку В плана механизма. Куда он будет вращать шатун 2 относительно точки А, в ту сторону и будет направлена угловая скорость шатуна ω₂.

Аналогично поступают со скоростью V _ВС. В каком направлении будет вращаться коромысло относительно точки С, туда и будет направлена угловая скорость ω₃.

План ускорений механизма и его свойства

Последовательность построения плана ускорений рычажного механизма аналогична построению плана скоростей. Рассмотрим её на примере механизма шарнирного четырехзвенника (рис. 2.2). Примем угловую скорость кривошипа постоянной (w₁ = const, что является наиболее распространённым и рациональным видом движения в реальных механизмах).

Векторное уравнение ускорений для звена 1 (кривошипа)

а _А= а _АО = а ⁿ_АО+ а ^t_АО ,

где нормальная составляющая ускорения точки A относительно O рассчитывается по формуле .

Вектор а ⁿ_АО параллелен отрезку АО на плане механизма. Тангенциальная составляющая ускорения а ^t_АО рассчитывается по формуле

.

В нашем случае угловое ускорение кривошипа e₁ = 0, тогда .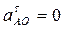

Векторное уравнение ускорений для звена 2 (шатуна)

а _В= а _А + а ⁿ_ВА+ а ^t_ВА,

где нормальная составляющая ускорения точки В относительно точки А рассчитывается по формуле .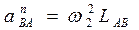

Вектор а ⁿ_ВА параллелен отрезку АВ и направлен от В к А, а тангенциальная составляющая а ^t_ВА перпендикулярна АВ.

Векторное уравнение ускорений для звена 3 (коромысла)

а _В= а _С + а ⁿ_ВС+ а ^t_ВС,

где ускорение точки С а _С = 0; нормальная составляющая ускорения точки В относительно точки С рассчитывается по формуле .

Вектор а ⁿ_ВС направлен параллельно отрезку ВС плана механизма от В к С, а вектор а ^t_ВС – перпендикулярно ВС.

Выбираем масштаб плана ускорений: , , где Р_аа^’ – длина отрезка, изображающего ускорение 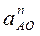на плане ускорений. Его длина выбирается произвольно из расчета, чтобы план ускорений разместился на отведенном месте чертежа и численное значение μ_а было удобным для расчетов (μ_а должно быть круглым числом).

Тогда ускорение а ⁿ_ВА будет изображаться на плане ускорений вектором, имеющим длину 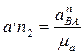, мм, а ускорение а ⁿ_ВС – вектором длиной 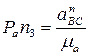, мм.

Затем строится план ускорений (рис. 2.2) с использованием составленных векторных уравнений ускорений. Из произвольно выбранного полюса Р_а параллельно отрезку ОА плана механизма проводится вектор ускорения 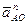, длина которого Р_аа′ была выбрана произвольно при расчете масштаба μ_а. Из конца этого вектора (точки а′) проводится вектор ускорения длиной а′n₂, который должен быть параллелен отрезку АВ плана механизма и направлен от точки В к точке А. Перпендикулярно ему через точку n₂ проводят прямую. Затем из полюса Р_а проводят вектор ускорения длиной Р_аn₃. Перпендикулярно ему через точку n₃ проводят прямую до пересечения с прямой, проведенной через точку n₂ перпендикулярно отрезку АВ. Точка пересечения обозначается буквой b′, которая, будучи соединена с полюсом Р_а, образует отрезок Р_аb′, изображающий вектор полного ускорения точки В.

Используя план ускорений, можно вычислить ускорения

,

Запишем

,

где w₂ и e₂ – угловые скорость и ускорение шатуна.

,

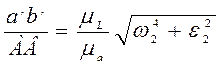где w₂ и e₂ не зависят от выбора (расположения) полюса Р_а плана ускорений, а отношение масштабов постоянно (m_L/m_a = const) для данного плана ускорений. Поэтому для любой точки (например, К, принадлежащей шатуну) можно записать пропорции

.

Отсюда формулируется теорема подобия: отрезки полных относительных ускорений на плане ускорений образуют фигуру, подобную соответствующей фигуре звена на плане механизма.

Величину ускорения точки К можно вычислить по формуле

.

Угловые ускорения звеньев шатуна , c^-1, направление e ₂ определяются по а ^t_ВА; угловые ускорения звеньев коромысла , c^-1, направление e ₃ – по а ^t_Вс.

Так как w ₂ и e ₂ направлены в противоположные стороны, вращение шатуна является замедленным.

Дата добавления: 2014-01-20