
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Билет16.ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
|
|
|
|
ОСНОВНЫЕ ТЕОРЕМЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА. Функция  называется оригиналом, если:
называется оригиналом, если:
1)  ;
;
2)  - кусочно-гладкая кусочно-непрерывная функция;
- кусочно-гладкая кусочно-непрерывная функция;
3) существует показатель роста, т. е. найдутся такие числа  и
и ,что
,что . (*)
. (*)
Наименьшее из чисел  или предел, к которому стремится наименьшее число, для которого справедливо равенство (*), называется абсциссой абсолютной сходимости и обозначается
или предел, к которому стремится наименьшее число, для которого справедливо равенство (*), называется абсциссой абсолютной сходимости и обозначается  . В дальнейшем под изображением
. В дальнейшем под изображением 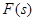 будем понимать:
будем понимать: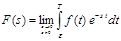 .
.
Такое уточнение изображения никак не сказывается на выполнении прямого и обратного преобразования Лапласа. Оно проявляет себя лишь в некоторых свойствах преобразования Лапласа.
Теорема 1.
Если  является оригиналом, то изображение
является оригиналом, то изображение 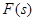 определено в области
определено в области  и является в этой области аналитической функцией.
и является в этой области аналитической функцией.
Первая часть теоремы, утверждающая существование изображения в области  , непосредственно следует из обобщенного преобразования Фурье. Докажем, что изображение
, непосредственно следует из обобщенного преобразования Фурье. Докажем, что изображение 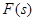 в этой области является аналитической функцией.
в этой области является аналитической функцией. 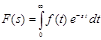 продифференцируем по s
продифференцируем по s
 .
.
Переходя к дифференцированию под знаком интеграла, получим
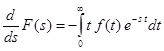 .
.
Покажем, что интеграл существует. Оценим



Т. о. получили, что интеграл существует, следовательно, производная существует при 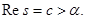
 можно взять сколь угодно близким числу
можно взять сколь угодно близким числу  . Отсюда следует, что
. Отсюда следует, что  существует в области
существует в области  Теорема доказана.
Теорема доказана.
Теорема 2(основная теорема об обратном преобразовании Лапласа).
Если функция  является оригиналом, а
является оригиналом, а 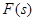 - изображение функции
- изображение функции  , то в каждой точке t непрерывности функции
, то в каждой точке t непрерывности функции 
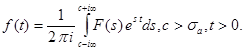
Доказательство этой теоремы следует из обобщенного преобразования Фурье. Она уточняет, что обратное преобразование Лапласа сходится к  только в точках непрерывности функции
только в точках непрерывности функции  . В точках разрыва
. В точках разрыва  обратное преобразование Лапласа сходится к среднему значению.
обратное преобразование Лапласа сходится к среднему значению.
Билет17.1. Линейность преобразований.
Теорема 1.
Если функция f1(t) и f2(t) являются оригиналами и имеют, соответственно, изображения F1(s) и F2(s), то преобразование Лапласа от соотношения
L[k1 f1(t) 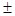 k2 f2(t)] = k1F1(s)
k2 f2(t)] = k1F1(s) 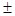 k2 F2(s),
k2 F2(s),
где k1, k2- некоторые константы.
Доказательство.
По определению преобразование Лапласа
L[k1 f1(t) 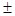 k2 f2(t)] =
k2 f2(t)] =
k1F1(s) 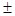 k2 F2(s).
k2 F2(s).
Замечание.
Из данной теоремы следует, что преобразование Лапласа линейной комбинации оригиналов равно той же линейной комбинации их изображений.
L[ ] =
] = 
 - const.
- const.
2. Изображение производной.
Теорема 2.
Если функции f(t) и f'(t) функция f(t) имеет изображение F[s], то преобразование Лапласа производной этой функции равно:
L[f(t)] = s F[s] – f(0+)
f(0+) = 
Теорема утверждает, что дифференцирование в вещественной области в комплексной области соответствует операции умножения изображения на s.
Доказательство.
По определению функция F[s] это: F[s] 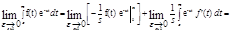


 ] =
] = 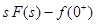
Покажем, что
 при с > α.
при с > α.
Последовательное применение теоремы 2 позволяет распространить ее на производную любого порядка.
 ] =
] = 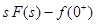
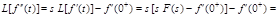

Продолжая процесс, можно установить, что для n-ой производной:
 3. Смещение в комплексной области.
3. Смещение в комплексной области.
Теорема 5.
Если функция f(t) оригинал и имеет изображение F(s), то

Доказательство.
По определению преобразование Лапласа

 .
.
Билет 18 Изображение интеграла.
Теорема 3.
Если функция f(t)-оригинал и имеет изображение F[s], то интеграл

также является оригиналом, причем
L[ ] = F(s)/s +
] = F(s)/s + 
L[ ] = F(s)/s +
] = F(s)/s +  /s.
/s.
Теорема утверждает, что интегрирование в вещественной области в комплексной области соответствует делению изображения на s (с точностью до const).
Доказательство. (2-ой части, которая приводит к формуле задания изображения).
По определению
F(s) = 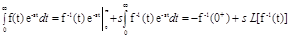
L[
Покажем, что
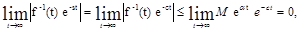 при
при  .
.
Теорема доказана.
4. Изменение масштаба.
Теорема 4.
Если функция f(t) оригинал и имеет изображение F(s), и «a» - некоторая положительная константа или положительная переменная независящая от t и s, то преобразование Лапласа:
L =
= 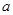

График функции  отличается от графика функции f(t) наличием масштаба по оси t.
отличается от графика функции f(t) наличием масштаба по оси t.
Доказательство.
По определению
F(W) = 
Положим,  имеем
имеем

Введем 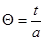 , тогда
, тогда 
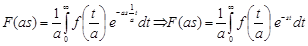
L =
= 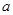
 .
.
Билет19.
Теорема 6.
Если функции f1(t) и f2(t) являются оригиналами и имеют соответственно изображения F1(s) и F2(s), то
L[ ] = F1(s)∙ F2(s)
] = F1(s)∙ F2(s)
Теорема утверждает, что произведению изображений в вещественной области соответствует интеграл свертки.
Доказательство.
Обозначим F(s) = L[ ]
]
По определению
F(s) = 
Верхний предел во внутреннем интеграле можно перенести из т. t в т. ∞, если подынтегральное выражение умножить на 1( ).
).
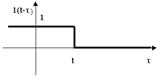
Рис. 1.
F(s) = 
Изменим порядок интегрирования
F(s) =
Принимая во внимание вид функции 1(t-τ) как функции аргумента t, запишем
F(s) =
Для второго интеграла введем подстановку  Отсюда следует, что
Отсюда следует, что
 ;
; 
F(s) = 
=


Рис. 2.
Замечание.
Может показаться на первый взгляд, что теорему свертки удобно использовать для вычисления обратного преобразования Лапласа. На самом деле это не так, интеграл свертки приводит к громоздким вычислениям.
7. Изображение запаздывающей функции.
Теорема 7.
Если функция f(t) является оригиналом и имеет изображение F(s), то преобразование Лапласа запаздывающей функции:
 при условии
при условии
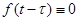 при t < τ. (*)
при t < τ. (*)
Доказательство.
По определению
F(s) = 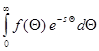
Положим 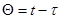 , тогда
, тогда 
F(s) = 
Принимая во внимание соотношение 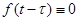 при t < τ нижний предел можно перенести из т. τ в т.0. Получим
при t < τ нижний предел можно перенести из т. τ в т.0. Получим
F(s) =  отсюда следует, что
отсюда следует, что

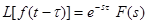 .
.
 Замечание 1.
Замечание 1.
По условию теоремы функция f(t) является оригиналом, следовательно, может быть записана в виде: f(t)·1(t). Запаздывающий оригинал имеет вид:
 , т. е. запаздывающий оригинал обязательно удовлетворяет условию (*).
, т. е. запаздывающий оригинал обязательно удовлетворяет условию (*).
 Замечание 2.
Замечание 2.
При пользовании данной теоремой во избежание ошибок оригинал следует записывать в виде f(t)·1(t).
f(t)·1(t).
Билет20. Предельный переход по второй независимой переменной.
Теорема 8.
Пусть а – переменная независящая от t и s. Если функция f(t,а) является оригиналом относительно переменной t и имеет изображение F(s,a), то при условии существования выписанных ниже пределов справедливо равенство:

Доказательство.
По определению
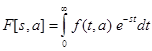
Перейдем к пределу


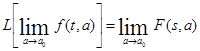
Используя эту теорему, найдем изображение δ - функции. Рассмотрим функцию f(t,a), изображенную на рисунке.

L[f(t,a)] = 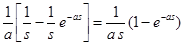
L[f(t- τ)] = 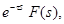 где
где 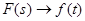
Рассмотрим предел
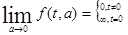
 т.о.
т.о. 
В соответствии с теоремой 8:
L[δ(t)] = 
Т. о. Получили L[δ(t)] = 1.
Для производной δ(t) справедливо соотношение
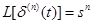
Это равенство формально может быть получено применением теоремы 2.
Для запаздывающей δ(t) справедливо соотношение
L[δ(t-τ)] = 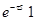
L[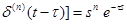 (в соответствии с теоремой 7).
(в соответствии с теоремой 7).
Билет21. Дифференцирование в комплексной области.
Теорема 9.
Если функция f(t) является оригиналом и имеет изображение F(s), то
L
Теорема утверждает, что дифференцирование изображений в вещественной области соответствует умножению оригинала на аргумент t.
Доказательство.
По определению
F(s) = 
Продифференцируем равенство по s. Это возможно, т. к. F(s)- аналитическая функция в области Re s >  .
.
 F(s) =
F(s) = 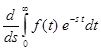
Перейдем к дифференцированию под знаком интеграла, получим
 F(s) =
F(s) = 
 L
L
В соответствии с таблицей

По теореме 9
L[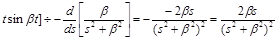
L[
Аналогично
L[
\
Билет 22. Предельное значение оригинала.
Теорема 10.
Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), и если произведение s F(s) является аналитической функцией в правой полуплоскости на мнимой оси, то
 .
.
Доказательство.
По теореме изображения производной

Перейдем пределу при 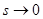 , данный предел существует, т. к. функция sF(s) – аналитическая в окрестности 0. Получим
, данный предел существует, т. к. функция sF(s) – аналитическая в окрестности 0. Получим



Переход к пределу под знаком интеграла возможен, т. к. по условию теоремы абсцисса абсолютной сходимости для функции 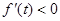 , поэтому
, поэтому
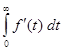 - существует.
- существует.
 наименьшее α - абсцисса абсолютной сходимости.
наименьшее α - абсцисса абсолютной сходимости.
Re s >  , α < 0.
, α < 0.
Из равенства
 следует, что
следует, что

 .
.
Для функции 
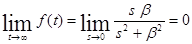

 - не существует.
- не существует.
Теорема не справедлива, т. к. функция  имеет два полюса на мнимой оси.
имеет два полюса на мнимой оси.
11.Начальное значение оригинала.
Теорема 11.
Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), то
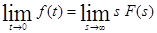
при условии, что 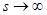 т. о., что Re s = c
т. о., что Re s = c .
.
Доказательство.
По определению
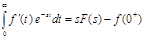
Перейдем к пределу

Покажем, что
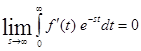
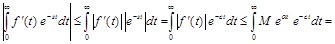

Справедливо равенство
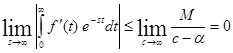
Из равенства

следует, что
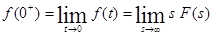
Билет24. Изображение решения линейного дифференциального уравнения имеет вид
 ,
,
где  - некоторые числа.
- некоторые числа.
Если  то дробь неправильная. Поделим числитель на знаменатель
то дробь неправильная. Поделим числитель на знаменатель

Принимая во внимание изображение  и ее производной, получим
и ее производной, получим

 - правильная дробь.
- правильная дробь.
Т. о. задача заключается в нахождении обратного преобразования Лапласа от правильной дроби.
В соответствии с формулой обратного преобразования Лапласа

Для вычисления интеграла воспользуемся леммой Жордана. Рассмотрим замкнутый контур L, изображенный на рисунке.
L = 

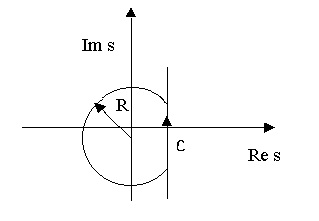

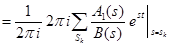
Вычеты берутся по всем точкам, лежащим левее прямой Re S = C.
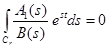
Тогда

В соответствии с основной теоремой (1) изображение является аналитической функцией в области Re S >  , т. к. C >
, т. к. C >  , то все особые точки функции
, то все особые точки функции  лежат левее прямой Re S = C, т. е. вычеты необходимо брать по всем особым точкам.
лежат левее прямой Re S = C, т. е. вычеты необходимо брать по всем особым точкам.
Рассмотрим два частных случая.
1. B(s) = 0, имеет простые вещественные корни.
Обозначим  корни уравнения B(s) = 0. Применяя формулу вычетов, найдем
корни уравнения B(s) = 0. Применяя формулу вычетов, найдем

2. Два корня являются мнимыми.
Пусть уравнение B(s) = 0, имеет корни

корни 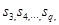 вещественные и простые.
вещественные и простые.
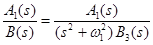
Изображение такого вида имеет место, когда в правой части дифференциального уравнения стоит гармоническая функция: sin или cos.
Применяя формулу 3 вычетов, найдем
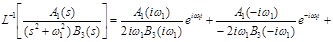

Два первых слагаемых комплексно сопряжены, поэтому при их суммировании мнимые части сокращаются, а вещественные удваиваются.


Иногда вместо операции взятия вещественной части удобно взять мнимую часть. Принимая во внимание, что
 ,запишем
,запишем
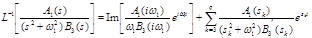
Замечание.
Полученные формулы можно использовать и в случае комплексных корней уравнения, однако в этом случае возникает необходимость выделять вещественную часть, что часто приводит к громоздким вычислениям. В этом случае целесообразно использовать разложение дроби на сумму простых дробей.
Билет 25. ИЗОБРАЖЕНИЕ ИМПУЛЬСА ПРОИЗВОЛЬНОЙ ФОРМЫ.
Рассмотрим функцию

Очевидно, что

По теореме линейности
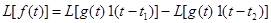
Обозначим 
Пусть  .
.
По теореме запаздывания

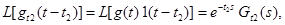 тогда
тогда
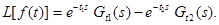 (1)
(1)
Пример.
Найти L[f(t)], если



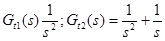
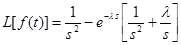 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1791; Нарушение авторских прав?; Мы поможем в написании вашей работы!