Системы с простой структурой

Алгоритм структурного анализа

1) в первую очередь обнаруживается диск с достаточным (не менее трёх) числом связей с «землей» и проверяется правильность наложения на него внешних связей сопоставлением с типовым способом 2 (при этом могут быть выявлены избыточные связи); в случае отсутствия такого диска целесообразно осуществить, если это возможно, предварительное укрупнение структуры системы путём соединения исходных дисков типовыми способами, в результате чего среди полученных крупных дисков могут появиться такие, у которых внешних связей достаточно для образования геометрически неизменяемой части системы;

2) если даже после укрупнения не удаётся обнаружить ни одного диска, геометрически неизменяемо соединённого с «землей», то выявляются два диска с не менее чем двумя внешними связями каждый, которые рассматриваются вместе с диском «земля» на предмет соединения по способу 3; если же и этот вариант первой операции синтеза не удаётся применить, то это означает, что система не может быть образована с помощью типовых способов и должны использоваться другие подходы (изложение их будет дано позднее);

3) далее производится присоединение других дисков, причем сначала рассматриваются возможности применения способов с более простыми наборами соединяемых объектов («диск-точка», «два диска») и лишь в последнюю очередь – приёмов соединения трёх дисков.

При выполнении каждой операции синтеза обязательно проверяется выполнение требований к расположению связей (табл. 3) – это позволяет обнаружить дефекты структуры расчётной схемы сооружения.

Если качественный анализ приводит к заключению об отсутствии структурных дефектов (наличие лишних связей к таковым не относится!), то делается вывод о геометрической неизменяемости системы; при этом в случае отсутствия лишних связей ГНС является статически определимой (количественный признак этого после выполнения структурного анализа – W = 0); а при W < 0 (есть лишние связи) – статически неопределимой.

При обнаружении дефектов структуры система квалифицируется как геометрически изменяемая или мгновенно изменяемая – в зависимости от того, какие перемещения – конечные или бесконечно малые могут возникать в ней из-за ошибок в расположении связей.

Таким образом, в результате выполнения структурного анализа даются ответы на все вопросы, обозначенные условными операторами 1, 2 и 3 в блок-схеме алгоритма кинематического анализа, приведённой на рис.1.6.

Системы, для которых качественный (структурный) анализ расчётной схемы может быть полностью выполнен с использованием только типовых способов (приёмов) геометрически неизменяемого соединения дисков, называются с и с т е м а м и с п р о с т о й с т р у к т у р о й.

Рассмотрим примеры структурного анализа плоских стержневых систем. Образование (синтез) рамы (см. рис. 1.30, а), для которой в результате количественного анализа получено W = – 3 (три избыточные связи), может быть представлено следующим образом:

1) диск D ₁ в виде ломаного стержня АРSB жёстко прикрепляется к диску «земля», что эквивалентно соединению двух дисков с помощью трёх связей (типовой приём 2а в табл. 3); результат этой операции – геометрически неизменяемая система (диск D _I = «земля» + D ₁) только с необходимыми связями, представленная на рис. 1.41, а, где штрихпунктирными линиями обозначены оси стержней в проекте сооружения;

Рис.1.41

2) к геометрически неизменяемой системе – диску D _I присоединяется диск D ₂ (ломаный стержень STD) – рис. 1.41, б – с помощью цилиндрического шарнира в точке Т и одной (вертикальной) из двух линейных связей, эквивалентных имеющейся в проекте сооружения шарнирной неподвижной опоре G; вторая линейная связь опоры пока что не используется; соединение соответствует типовому приёму 2б, причём требование к связям выполняется: направление оси линейной связи не проходит через шарнир Т; результат операции – диск D _II = D _I + D ₂ , образованный с помощью только необходимых связей и включающий в себя диск «земля», следовательно, полученная на этом шаге синтеза система – геометрически неизменяемая и не имеющая избыточных связей;

3) к геометрически неизменяемой системе – диску D _II присоединяется диск D ₃ (стержень KL) – рис. 1.41, в – с помощью двух цилиндрических шарниров в точках K и L, суммарно эквивалентных четырём линейным связям, из которых одна – избыточная, так как типовые приёмы соединения двух дисков по способу 2 (см. табл. 3) требуют лишь трёх связей; в качестве избыточной может рассматриваться, например, горизонтальная линейная связь в эквивалентном представлении шарнира L, тогда шарнир K и вертикальная связь в точке L обеспечивают правильное прикрепление диска D ₃ к диску D _II типовым приёмом 2б; результат – геометрически неизменяемая система (диск D _III) с одной избыточной связью; к этому же заключению можно прийти другим путём – рассматривая стержень KL в качестве линейной связи, соединяющей точки одного и того же диска, – в этом случае она является избыточной;

4) в геометрически неизменяемую систему (диск D _III) с одной избыточной связью вводятся оставшиеся неиспользованными предусмотренные исходной расчётной схемой сооружения две линейные связи – вертикальная и горизонтальная в опорах В и G соответственно (см. рис. 1.41, г); получается система, схема которой совпадает с заданной, с тремя избыточными связями;

5) проверяя избыточные связи (1 – вертикальную в точке В, 2 – горизонтальную в точке G и 3 – стержень KL) по критериям 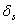=? и 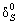=? с определением возможных перемещений в системе с одновременно удалёнными всеми избыточными связями в количестве n _изб.св. = – W = 3 (см. рис. 1.41, б), находим, что с использованием гипотезы отвердения 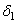= 0, = 0 и 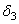= 0, а с учётом деформаций 0, 0 и 0, следовательно, все избыточные связи – лишние;

6) вывод: заданная система геометрически неизменяемая, с простой структурой, с тремя лишними связями, т.е. статически неопределимая.

Приведённое выше пошаговое изображение расчётной схемы системы в процессе её синтеза (см. рис. 1.41) не является обязательным – оно может быть полезным на начальной стадии выработки навыков выполнения кинематического анализа (в дальнейшем заменяясь соответствующими мысленными представлениями), а также в затруднительных случаях исследования структуры многоэлементных систем.

Вместо подробного описания процедуры качественного анализа можно применять сокращённую запись; в частности, для рассмотренного примера:

1) «земля» + D ₁ = D _I – по способу 2 (приём 2а – соединение двух дисков с помощью трёх связей 1-го типа в форме неподвижной защемляющей опоры) ГНС только с необходимыми связями;

2) D _I + D ₂ = D _II – по способу 2 (приём 2б – соединение двух дисков с помощью шарнира S и линейной связи в точке G; ось связи не проходит через центр шарнира) ГНС только с необходимыми связями;

3) D _II + D ₃ = D _III – соединение двух дисков с помощью двух цилиндрических шарниров (четырёх эквивалентных простых связей; одна связь – избыточная) ГНС с одной избыточной связью;

4) D _III + две линейные связи в точках В и G = геометрически неизменяемая система с тремя избыточными связями;

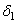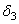5) для группы из трёх избыточных связей (п. 3 и 4): = 0, = 0, = 0, 0, 0, 0 все три связи – лишние;

6) вывод: заданная система геометрически неизменяемая, с простой структурой, с тремя лишними связями, т.е. статически неопределимая.

Для системы, представленной на рис. 1.42, количественный анализ дает

W = ==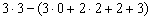 0

(D = 3 – стержни АРС, СSВ и СК; П = 0; Н = 2 – кратный шарнир С; С = 2 – стержни АК и КВ; С _о = 3).

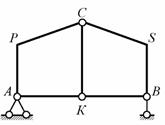
Рис.1.42

Следовательно, система может быть геометрически неизменяемой, и структурный анализ необходим.

В системе имеются три внешние связи (две шарнирные опоры), но ни у одного из исходных дисков нет трёх связей с «землей». Поэтому для того, чтобы система была геометрически неизменяемой, нужно, чтобы соединённые друг с другом её элементы образовывали бы единый диск. Для проверки этой возможности выполняем предварительное укрупнение структуры. Используя иное, чем в количественном анализе, представление о дисках и связях, синтез системы осуществляем следующим образом:

1) (D ₁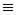 АРС) + точка К = D _I – по способу 1 (прикрепление точки к диску с помощью двух линейных связей – стержней АК и СК, направления осей которых не совпадают);

2) D _I + (D ₂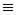 СSB) + (D ₃ 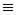КB) = D _II – по способу 3 (приём 3б – соединение трёх дисков с помощью трёх цилиндрических шарниров С, В и К, не лежащих на одной прямой);

3) D _II + «земля» = ГНС – по способу 2 (приём 2а – соединение двух дисков с помощью трёх линейных связей, оси которых не сходятся в одной точке и не параллельны);

4) вывод: рассмотренная система геометрически неизменяемая, с простой структурой, статически определимая (W = 0).

Возможны варианты: например, соединение стержней АРС, СК и АК в диск D ₁ можно рассматривать по способу 3 (три диска и три шарнира А, С, К), а образование диска D _II – по способу 2 (D ₁ и CSB с помощью шарнира С и связи КВ – приём 2б); перед соединением диска D _II с «землей» можно предварительно прикрепить к «земле» точку А по способу 1, а затем к двум дискам (D _II и «земля» + (^.) А) применить приём 2б (соединение цилиндрическим шарниром А и линейной связью в точке В.

Количественный анализ системы со схемой по рис. 1.43, а показывает, что система может быть геометрически неизменяемой (если к дискам отнести стержни КС и СР, а остальные стержни считать связями 1-го типа, то D = 2, П = 0, Н = 1, С = 0, С _о = 4, тогда W =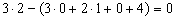– необходимое условие геометрической неизменяемости выполняется).

Рис.1.43

Структурный анализ начинается с поиска диска, имеющего три связи с «землей». Таких дисков в системе нет. Поэтому первым шагом синтеза не может быть соединение двух дисков, одним из которых является «земля». Предварительное укрупнение структуры системы невозможно – нет ни одной пары дисков, которые могли бы быть объединены типовыми способами. Следовательно, нужно оценить возможность соединения трёх дисков – таковыми оказываются «земля» и стержни КС и СG, связанные по способу 3 – тремя шарнирами, из которых один реальный (С), а два других – фиктивные (А и В). Шарниры А, В и С не лежат на одной прямой, следовательно, система имеет правильную структуру и является геометрически неизменяемой, а ввиду отсутствия избыточных связей (W = 0) – статически определимой.

На примере рассмотренной системы можно убедиться в необходимости внимательной проверки выполнения требований к расположению связей. Так, если изменить углы наклона внутренних стержней, то положение фиктивных шарниров (точек А и В) изменится, и они могут оказаться на одной прямой с шарниром С (см. рис. 1.43, б), а это – характерный признак мгновенно изменяемого соединения дисков, вследствие чего и система в целом должна быть квалифицирована как мгновенно изменяемая.

В расчётной схеме сооружения, показанного на рис. 1.44, дисками могут считаться стержни АС, СВ, GК, KL, LP и РS (D = 6), тогда H = 4 (простые шарниры в точках С, К, L и Р), С = 3 (внутренние линейные связи ЕК, CL и ТР), П = 0, С _о = 7 (две опорные связи в точке А, одна в точке В и по две в точках G и S). Характеристика W =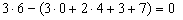– необходимое условие геометрической неизменяемости системы выполняется.

Рис.1.44

Но попытки осуществить синтез системы с помощью типовых способов оказываются безуспешными – это невозможно, так как все диски должны соединяться друг с другом и с диском «земля» одновременно, чтобы в результате обеспечить геометрическую неизменяемость (а система в действительности обладает этим качеством, но доказать это простейшими способами нельзя).

Дата добавления: 2014-01-11